写在前面:该算法
- 目的是在比HUI-Miner算法更高效率,关键在于两个新上界:revised sub-tree utility、local utility来压缩高效检索空间。
- 并且通过快速效用值计算算法FAC(Fast Utility Counting)来在线性时间内获取上界值和检索空间。
- 更进一步,通过HDP(High-utility Database Projection)和HTM(High-utility Transaction Merging)在线性时间内完成对数据库的映射和事务归并
EFIM: A Fast and Memory Efficient Algorithm for High-Utility Itemset Mining
样本



定义
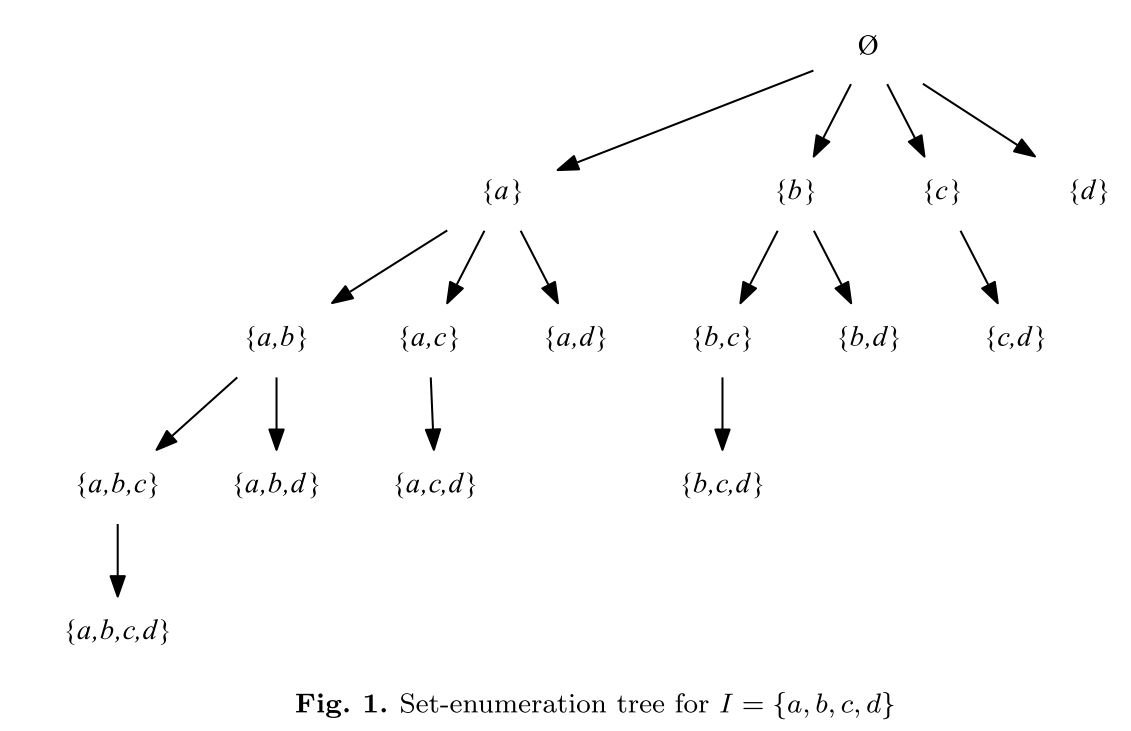
$E(\alpha)$:表示根据深度优先搜索遍历所有项,得到大于 $\alpha$ 的所有项集,有$E(\alpha)$ = {$ z \mid z \in I \land z \succ x, \forall x \in \alpha$},如Fig.1,设 $\alpha$ = $\lbrace c\rbrace$,则 $E(\alpha)$ = $\lbrace a, b, d\rbrace$
扩展项集(Extension of an itemset):设项集Z是项集$\alpha$的扩展,若 $Z = \alpha \cup W$ 且$W \in 2^{E(\alpha)}$,则有$W \ne \varnothing$且$Z$是项集$\alpha$的子树和枚举树
一元扩展项集(Single-item extension of an itemset):设项集Z是项集$\alpha$的一元扩展,若$Z = \alpha \cup W$,则$Z$是项集$\alpha$的子树和枚举树
Ps.例子:假设$\alpha$ = $\lbrace d \rbrace$, $E(\alpha)$ = $\lbrace e, f, g \rbrace$,那么一元扩展项集就是 $\lbrace d, e\rbrace、\lbrace d, f\rbrace、\lbrace d, g\rbrace$,多元扩展集为 $\lbrace d, e, f\rbrace、\lbrace d, f, g\rbrace、\lbrace d, e, f, g\rbrace$
映射事务(Projected transaction):由 $\alpha$-$T$ = $\lbrace i \mid i \in T \land i \in E(\alpha) \rbrace$表示,其中T是事务项,$\alpha$是项集,$E(\alpha)$是扩展项集(处理一行事务项,也就是该事务项排在项集α的之后的项组成的新的事务项)
映射数据库(Projected database):由 $\alpha$-$D$ = $\lbrace \alpha$-$T \mid T \in D \land \alpha$-$T \ne \varnothing \rbrace$表示,其中D是数据库,$\alpha$是项集,T是事务表(处理多行事务项,也就是对整个事务表进行映射事务处理,组成一个新的数据库)
Ps. 当某交易项不包含指定的项集α,那么在映射过程中会删除这个交易项
相同的事务(Indentical transaction):当 $T_a、T_b$ 两个交易项的所有的项元素都相同时,我们认为事务项$T_a$和事务$T_b$是相同的事务
归并事务(Transaction merging):当在数据库D中存在相同的事务项$T_{r1}、T_{r2} \dots T_{rm}$时,我们设置一个新的事务$T_M$来替代这些,且每项 $i \in T_M$ 都被定义为 $q(i, T_M) = \sum_{k = 1 \dots m}q(i, T_{rk})$
映射归并交易(Projected transaction merging):在映射数据库 $\alpha$-$D$ 中,将所有重复的事务项 $T_{r1}、T_{r2}、\dots T_{rm}$用一个新的事务项 $T_M$ 来替代,且每项 $i \in T_M$ 都被定义为 $q(i, T_M) = \sum_{k = 1 \dots m}q(i, T_{rk})$
交易项总顺序(Total order on transactions):我们用 $\succ_T$ 来表示,有以下四种情况则判定成立:
- $T_b$ 的TID全都大于 $T_a$ 的TID,则$T_b \succ T_a$
- 当 $k > m$ 且 $i_{m-x} = j_{k-x}$ 且对 $\forall x \in Z, 0 \le x < m$,则 $T_b \succ_T T_a$
- 当 $\exists x$ 且 $0 \le x < y < min(m, k)$,有 $j_{k-x} \succ i_{m-y}$ 和 $i_{m-y} = j_{k-y}$ 成立,则 $T_b \succ_T T_a$
- 其它情况是 $T_a \succ_T T_b$
剩余效用边界(remaining utility upper-bound):这个概念是区别于“两步走”算法的关键之处,因为这个边界值比 TWU 是更为紧凑,能够裁剪更精细。定义为 $reu(X) = re(X) + u(X)$
定理:
如果reu(X)<minutil,则项集X和它的超集都是低效用值项集
证明:
设项集X和它的超集Y,事务项T,其中有关系 $X \subset Y \subseteq T \Rightarrow (Y \setminus X) \subseteq (T \setminus X)$当把所有包含项集X的事务项都计算起来,自然可知当 reu(X) < minUtil,那么超集必然也小于,那么
$u(Y, T) = u(X, T) + u(Y \setminus X, T) = u(X, T) + \sum_{i \in (Y \setminus X)}u(i, T)$
$\le u(X, T) + \sum_{i (\in T \setminus X)}u(i, T) = u(X, T) + re(X, T) = reu(X, T)$
Ps. 结合上面的定义9也可以看出来,其实 Y\X 就是所有大于项(集)X的项组成的剩余项集
第一阶梯项(Primary items):设存在项集 $\alpha$,那么有 $Primary(\alpha) = \lbrace z \mid z \in E(\alpha) \land su(\alpha, z) \ge minuti\rbrace$
第二阶梯项(Secondary items):设存在项集 $\alpha$,那么有 $Secondary(\alpha) = \lbrace z \mid z \in E(\alpha) \land lu(\alpha, z) \ge minutil \rbrace$
修正子树效用值(Redefined Sub-tree utility):设存在项集 $\alpha$ 和项 $z$,重新定义的 $su(\alpha, z) = \sum_{T \in g(\alpha \cup \lbrace z\rbrace)}[u(\alpha, T) + u(z, T) + \sum_{i \in T \land i \in E(\alpha \cup \lbrace z\rbrace \land i \in Secondary(\alpha))}u(i, T)]$
Ps.因为有 $lu(\alpha, z) \ge su(\alpha, z)$,所以 $Primary(\alpha) \subseteq Secondary(\alpha)$,意味着只需检索以 $Primary(\alpha)$ 中的子项集与 $\alpha$ 的并集为根结点的子树,且其它项集不做考虑。例如项 α = {a},Primary(α) = {c, e},Secondary(α) = {c, d, e},这意味着对于项集 α,我们只要检索以 α∪{c} 和 α∪{e} 为根节点的子枚举树,并且在这两个枚举树中,除了项c、d、e,其它的项都不考虑
四个关键点
- 需要设计一种单一算法来避免因产生候选项集问题 $\Rightarrow$ Utility List
- 通过使用“模式增长方法”来避免多花时间去考虑数据库中那些可能不会出现的模式,而且算法要减少对数据库的扫描 $\Rightarrow$ HDP & HTM
- 通过设计一个紧凑的上界来缩小检索空间,且这个上限应该比当下算法中通过保留有效上界更紧凑 $\Rightarrow$ local utility & revised sub-tree utility
- 算法在时间和空间上的操作都要尽可能地简单 $\Rightarrow$ FUC
HDP(High-utility Database Projection)
采用该技术的目的是通过某个项来投影出更小的数据库,达到减少扫描量的效果
原理:
当一个项集$\alpha$出现在深度优先遍历结果中,存在项集$x \notin E(\alpha)$时,通过扫描数据库在$\alpha$的子树或效用值上界中,可以不用计算这些项集x的效用值。我们称这种删除后的数据库为投影数据库(projected database),同理还有投影事务(projected transaction)
方法:
- 按照“$\succ$”关系对源数据库的每个交易项目进行升序排序
- 每个投影事务由对应的源交易上的偏移指针来表示,也称为伪投影
HTM(High-utility Transaction Merging)
采用该技术的目的通过减小数据库规模来减少对数据库扫描的开销
原理:
交易数据库中常常包含重复的交易信息(Identical transaction),本技术需要找出这些相同的交易信息,然后在梳理它们效用值得过程中只保留一条交易信息
方法:
- 找出相同的交易信息(Identical transaction),进行归并处理,用一个新的交易项 $T_M$ 来代表这些重复的
- 对映射数据库做同样的处理,称为映射归并交易(Projected transaction merging)
- 最后得出交易总订单(Total order on transaction),这之间的交易项集是按序从小到大排列
Ps.以上两个技术是配套使用的:“归并 -> 投影 -> 归并 -> 投影 -> …”,一边通过归并使得共同前缀不断增长(上界),一边投影事务表(缩小,因为有共同前缀,那么前缀就可以暂时不考虑)
排序$\succ_T$
其实在每次投影开始前,都要对交易表进行交易项排序,这样是在一定程度上提高投影和归并效率,不必重复扫描数据项
排序判定有以下四个标准,我们设有交易项 $T_a = \lbrace i_1, \cdots, i_m\rbrace, T_b = \lbrace j_1, \cdots, j_k\rbrace$:
当 $m = k, \forall x \in [0, m \mid k]$,有 $i_x = j_x$,但是 b > a,则 $T_b \succ_T T_a$(翻译一下就是从后往前依次对比两个交易项的各项元素,发现两个交易项一模一样,差别就是交易项b的角标数字大于交易项a,所以交易项b大于交易项a)
- 当 $\forall x \in [0, m)$,若 $k > m, i_{m-x} = j_{k - x}$,则 $T_b \succ_T T_a$(翻译一下就是从后往前依次对比两个交易项的各项元素都相等,但交易项a没交易项b长,所以交易项b大于交易项a)
- 当 $\forall x \in [x, min(m, k)), y \in (x, min(m, k))$,有 $i_{m-y} = j_{k-y}, j_{k-x} \succ i_{m-x}$,则 $T_b \succ_T T_a$(翻译一下就是从后往前依次对比两个交易项的各项元素,发现比到一个位置n这两个项元素有 $j_n \succ i_n$,所以交易项b大于交易项a,类似于比较字符串字串大小一样)
- 其它情况统统设定为 $T_a \succ_T T_b$
以下两个概念是定义了新的上边界值,不同于 Remain Utility 和 Transaction Weighted Utilization 这两个上边界值,他们分别是在搜索枚举树中的项目集α的子树中定义的,时刻动态变化的上界值,而不是像twu这样的定值,所以新提出的上界值会更紧凑,对检索空间的有效删减程度更大
Local utility
定义:
设项集 $\alpha$ 和项 $z \in E(\alpha)$,有 $lu(\alpha, z) = \sum_{T \in g(\alpha \cup \lbrace z\rbrace)}[u(\alpha, T) + re(\alpha, T)]$,例如:设 $\alpha = \lbrace a\rbrace$,则有 $lu(\alpha, c) = (8+27+30), lu(\alpha, d) = 30, lu(\alpha, e) = 57$(通过观察Table 1,你会发现 $lu(a, c) = TU(T_1) + TU(T_2) + TU(T_3)$,当然这只适用于排在第一位的项,比如对于项 {c} 就不是这样的了,有没有对 {c} 计算更简便的方法,利用前面已经算出来的值?)
定理:
设存在项集 $\alpha$ 和项 $z \in E(\alpha)$,且有 $z \in Z$,其中 $Z$ 是 $\alpha$ 的扩展集,对于 $lu(\alpha, z) \ge u(Z)$ 仍然成立,故当 $lu(\alpha, z) < minutil$ 时,在项集 $\alpha$ 的扩展项集中所有包含项 z 的项集都是低效用值,简而言之就是在遍历 $\alpha$ 的子树中,可以忽略掉项 z 和项集 α 为根节点的子树
证明:
设 项集 Y = α ∪ {z},项集Z 的效用值定义为 $u(Z) = \sum_{T_{\rm c} \in g(Z)}u(Z, T_{\rm c}) = \sum_{T_{\rm c} \in g(Z)}[u(\alpha, T_{\rm c}) + u(Z \setminus \alpha, T_{\rm c})]$,那么项集α 的局部效用值(local utility)就为 $lu(\alpha, z) = \sum_{T_{\rm c} \in g(Y)}[u(\alpha, T_{\rm c}) + re(\alpha, T_{\rm c})]$(这个公式是不是很像reu = iutils + rutils???)。原因在于 $g(Z) \subseteq g(Y)$ 且 $Z \setminus Y \subseteq E(\alpha)$,故必有 $u(Z \setminus \alpha, T_{\rm c}) \le re(\alpha, T_{\rm c})、u(Z) \le lu(\alpha, z)$
Ps. 其实这部分证明只要对着上图中的枚举树(图Fig. 1.),把上述公式套进去就很容易看出来
Sub-tree utility
定义:
设有一个项集 $\alpha$ 且有一个项 $z$ 可以对 $\alpha$ 通过深度优先遍历进行扩展,其中 $z \in E(\alpha)$,那么有 $su(\alpha, z) = \sum_{T \in g(\alpha \cup \lbrace z\rbrace)}[u(\alpha, T) + u(z, T) + \sum_{i \in T \land i \in E(\alpha \cup \lbrace z\rbrace)}u(i, T)]$,例如:设 α = {a},则有 $su(\alpha, c) = $
$ [u(a, T_1) + u(c, T_1) + u(d, T_1)] + $
$[u(a, T_2) + u(c, T_2) + u(e, T_2) + u(g, T_2)] + $
$[u(a, T_3) + u(c, T_3) + u(d, T_3) + u(e, T_3) + u(f, T_3)] $
$ = 61 $ $su(\alpha, d) = 25, su(\alpha, e) = 34$ 定理:
1.设存在项集 $\alpha$ 和项 $z \in E(\alpha)$,对于 $su(\alpha, z) \ge u(\alpha \cup \lbrace z\rbrace)$ 仍然成立,并且有 $su(\alpha, z) \ge Z \land Z \subseteq \alpha \cup \lbrace z\rbrace$,故当 $su(\alpha, z) < minutil$ 时,在一元项集 $\alpha \cup \lbrace z\rbrace$ 和它的扩展集都是低效用值,简而言之可以剪去枚举树中的 $\alpha \cup \lbrace z\rbrace$ 子树
2.设存在项集 $\alpha、Y = \alpha \cup \lbrace z\rbrace$ 和项 $z$,则存在不等式 $twu(Y) \ge lu(\alpha, z) \ge reu(Y)$ = $su(\alpha, z)$
证明:
1.设项集 Y = α ∪ {z},那么 $u(Y) = \sum_{T_c \in g(Y)}u(Y, T_c)$,
$su(\alpha, z) = \sum_{T_c \in g(Y)}[u(\alpha, T_c) + u(z, T_c) + \sum_{i \in T_c \land i \in E(\alpha \cup \lbrace z\rbrace)}u(i, T_c)]$
$= \sum_{T_c \in g(Y)}u(Y, T_c) + \sum_{T_c \in g(Y)}\sum_{i \in T \land \in E(\alpha \cup \lbrace z\rbrace)}u(i, T_c)$
$\ge \sum_{T_c \in g(Y)}u(Y, T_c) = u(Y)$
2.设项集Z是项集Y的扩展,那么 $u(Z) = \sum_{T_{\rm c} \in g(Z)}u(Y, T_{\rm c}) + \sum_{T_{\rm c} \in g(Z)}u(Z \setminus Y, T_{\rm c})$,因为有 $g(Z) \subseteq g(Y),Z \setminus Y \subseteq E(\alpha)$,故有 $su(\alpha, z) \ge u(Z)$
下图表示EFI-Ming算法的裁剪优势:
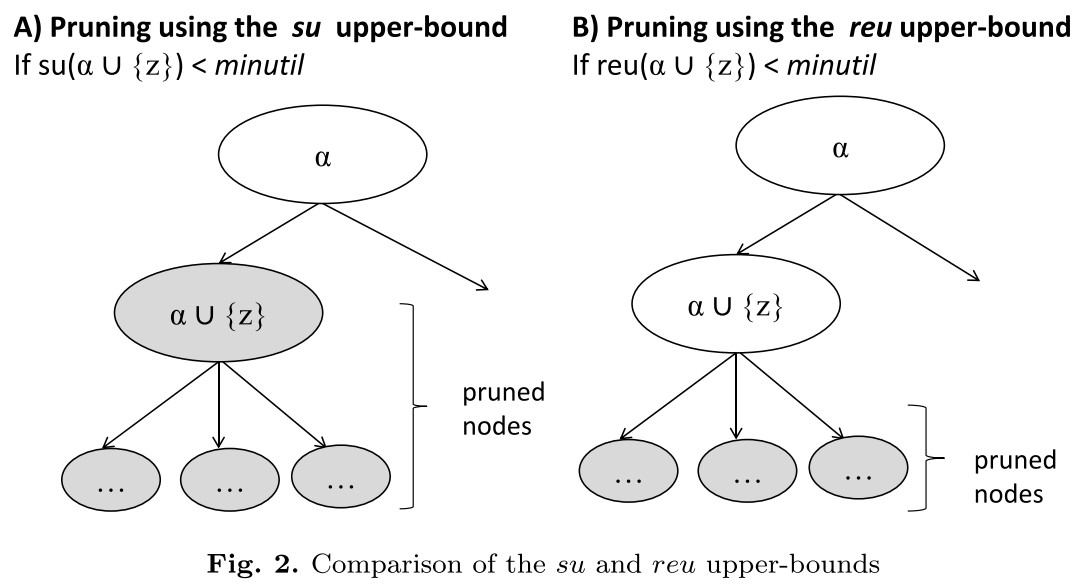
FUC(Fast Utility Counting)
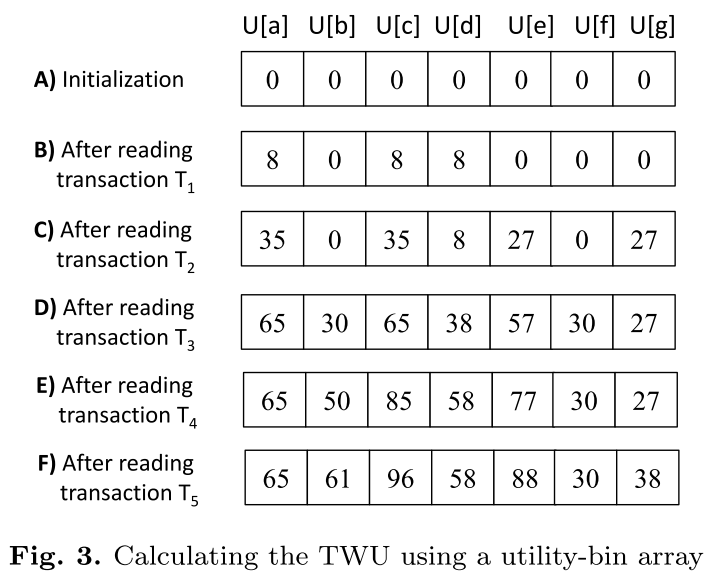
采用该剪枝技术的目的是通过一种数组结构(utility-bin)在线性时间和空间内计算出上界
定义:
效用箱(utility-bin):设 I 是数据库中的一个项集,效用箱数组 U 的长度为length(I),在数组 U 中每项表示为 U[z]$(z \in I)$,数组内存储的是效用值,效用箱数组通常是用来在O(n)时间复杂度内去高效计算上界值
使用:
利用utility-bin计算$twu(X)$,有公式 $U[z] = U[z] + tu(T)$,其中 $z \in T$,在处理完最后一个事务时,对于 $\forall i \in I,twu(i) = U[i]$
下图是个示例:

利用utility-bin计算$su(\alpha, T_j)$,对于项集 α,
有公式 $U[z] = U[z] + u(\alpha, T_j) + u(z, T_j) + \sum_{i \in T_j \land i \succ z \land i \in Secondary(\alpha)}u(i, T_j)$,其中 $z \in T_j \land E(\alpha)$,在处理完最后一个事务时,对于 $\forall i \in E(\alpha), U[i] = su(\alpha, i)$
利用utility-bin计算$lu(\alpha, T_j)$,对于项集 α,有公式 $U[z] = U[z] + u(\alpha, T_j) + re(\alpha, T_j)$,其中 $z \in T_j \land E(\alpha)$,在处理完最后一个事务时,对于 $\forall i \in E(\alpha), U[i] = lu(\alpha, i)$
关键算法实现


个人总结
花了很长时间去研究这个算法,不得不说很多地方设计得很精彩,例如使用utility-bin来使得twu的计算控制在线性范畴内,local utility和sub-tree utility能得出更紧凑的上界。而且很多实现细节地方没有源码光看论文是真的没思路,思路可以认为是先构造一元项的枚举树,这里是第一次缩减检索空间;然后围绕枚举树,开始对事务表进行操作;通过检查出的共同前缀,来进进一步对枚举树进行删减,这是第二次缩减检索空间;利用共同前缀,对项e进行一个个扩展(增长模式法),留下符合的项集并输出,删除不符合条件的;重复进行以上过程最终枚举树无法延伸即可结束。在这个过程中还有各种参数的转换、留存,详情可以查找源代码。
最后同时也非常感谢郭大佬的总结报告,有些不明朗的地方听了他的讲述一下子就通了。个人功底还是欠缺,对论文中的要点理解不到位,往后多加学习如何分析论文。
参考
- EFIM算法演示教程-http://www.philippe-fournier-viger.com/spmf/EFIM.php
- Souleymane Zida、Philippe Fournier-Viger、Jerry Chun-Wei Lin、Cheng-Wei Wu、Vincent S. Tseng:EFIM: A Fast and Memory Efficient Algorithm for High-Utility Itemset Mining-http://philippe-fournier-viger.com/EFIM_JOURNAL_VERSION%20KAIS%202016.pdf
- EFIM原作的ppt-http://www.philippe-fournier-viger.com/EFIM_and_EFIM-Closed_high_utility_mining.pdf