写在前面:在老师介绍这篇文章的时候确实让我眼前一亮,为什么之前自己就没有联系到存在负效用情况?看来自己对这些算法理念还是没有融会贯通,这些算法都是为生活服务的。本篇记录对EHIN文献上翻译的个人理解,如有错误还望指正。
HUIs with Negative utility algorithm
EFIM中的定义
设 $I$ = $\lbrace I_1, I_2, \cdots, I_m\rbrace$ 是一组含不同元素的项(可以看作是用户的多组购物商品),集合 $X \subseteq I$ 称作项集 。
设 $D = \lbrace T_1, T_2, \cdots, T_n\rbrace$ 是一组含不同交易的数据集(可以看作是用户的多次购物记录)。
有 $\forall X_i \in I$,有内部效用(Internet Utility,购物数量)$IU(X_i, T_i)$(参照Table 1)和额外效用(External Utility,商品利润)$EU(X_i)$(参照Table 2),其中 $EU(X_i)$ 可能是正值也可能是负值。
Table 1 交易数据库
TID Transaction $T_1$ (a, 2) (b, 2) (d, 1) (e, 3) $T_2$ (b, 1) (c, 5) (e, 1) $T_3$ (b, 2) (c, 2) (d, 3) (e, 2) $T_4$ (c, 2) (d, 1) (e, 3) $T_5$ (a, 2) $T_6$ (a, 2) (b, 1) (c, 4) (d, 2) (e, 1) $T_7$ (b, 3) (c, 2) (e, 2) Table 2 各项的额外效用值
Item a b c d e External Utility 2 -3 1 4 1 对 $\forall X_i \in T_j$,有对应的项效用(Utility of an Item) $U(X_i, T_j) = IU(X_i, T_j) \times EU(X_i)$。比如 $U(a, T_1) = IU(a, T_1) \times U(a) = 2 \times 2 = 4$
对 $\forall X \subseteq T_j$ ,有在一组交易项中项集对应的效用 $U(X, T_j) = \sum_{X_i \in X \land x \subseteq T_j}U(X_i, T_j)$。比如 $U(\lbrace a, d\rbrace, T_1) = U(a, T_1) + U(d, T_1) = 2 \times 2 + 1 \times 4 = 8$
对 $\forall X \in D$,有该项集在所有相关交易项的效用 $U(X) = \sum_{X \subseteq T_j \in D}U(X, T_j)$。比如 $U(\lbrace a, d\rbrace) = U(\lbrace a, d\rbrace, T_1) + U(\lbrace a, d\rbrace, T_6) = (4 + 4) + (4 + 8) = 20$
高效用项集(HUI),指的是该项集 $U(X) \ge minUtil > 0$,否则就是 $low \; high \; utility$
比如我们设阈值(minUtil = 10),那么根据上表和定义可以计算出所有的HUIs为下表所示:
Table 3 高效用项集
Itemset Utility Itemset Utility {a} 12 {c} 14 {a, c, d} 16 {c, d} 31 {a, c, d} 13 {c, d, b} 16 {a, c, d, e} 17 {c, d, e} 37 {a, c, d, e, b} 14 {c, d, e, b} 19 {a, d} 20 {c, e} 23 {a, d, b} 11 {d} 28 {a, d, e} 24 {d, e} 37 {a, d, e, b} 15 {d, e, b} 15 {a, e} 12 {e} 12 对 $\forall T_j \in T$,每个交易项的效用(Transaction Utility) $TU(T_j) = \sum^{m}_{i}U(X_i, T_j)$,其中 m 是指交易项中包含的项集数目。比如 $TU(T_1) = U(a, T_1) + U(b, T_1) + U(d, T_1) + U(e, T_1) = 4 + (-6) + 4 + 3 = 5$
对 $\forall X \in D$,每个项集在所有相关事务中的交易项权重效用(Teansaction Weighted Utility) $TWU(X) = \sum_{X \subseteq T_j \in D}TU(T_j)$.比如 $TWU(a) = TU(T_1) + TU(T_5) + TU(T_6) = 5 + 5 + 14 = 23$
Ps. 存在性质:若 TWU(X) < minUtil 时,那么项集 X 和它的超集都不属于 HUIs 集合(言外之意就是我们可以用这个性质来进行剪枝,用这个对一元项集进行第一轮删减效果最佳)这里需要补充一点:TWU默认所有项集的效用值都是正,因此在面对负值的情况需要做一定的修改。
修正交易项效用(Redefined Transaction Utility)$RTU(T_j) = \sum^{m}_{i \in Tj \land EU(X_i) > 0}U(X_i, T_j)$,其中 m 是指交易中包含的项集数目。比如 $RTU(T_2) = U(c, T_2) + U(e, T_2) = 5 + 1 = 6$,这其中只计算正效用值,所以有 $RTU(T_j) \ge TU(T_j)$,因为 TU 里还包含了负效用项的值。
修正交易项权重效用(Redefined Transaction Weighted Utility)$RTWU(X) = \sum_{X \subseteq T_j \in D}RTU(T_j)$。比如 $RTWU(a) = RTU(T_1) + RTU(T_5) + RTU(T_6) = 11 + 4 + 17 = 32$,下表可作参考:
Table 4 修正的各项权重效用值
Item a b c d e RTWU 32 53 51 52 62 Ps.在近些年已经有人使用 RTU 来查找那些包含负值的HUIs,EHIN算法也使用 utility-list 来计算包含负效用项集的保留效用(Remaining Utility),但不使用 utility-list 那套数据结构来存储正(负)效用项(集)
每个项集 X 的效用列表(Utility-List)中每行是一个包含项集 X 交易项,而每个交易项有三个参数:tid、iutil、rutil,其中 $iutil = U(X, T_j), rutil = RU(X, T_j)$。比如项集{a} 的效用列表就为 $[(T_1, 4, 7), (T_5, 4, 0), (T_6, 4, 13)]$,容易得 U({a}) = (4 + 7) + (4 + 0) + (4 + 13) = 32;项集 {a, d} 的效用列表为 $[(T_1, 8, 3), (T_6, 12, 1)]$,故 U({a, d}) = (8 + 3) + (12 + 1) = 24
Ps. 这是不包含负值计算的结果,EHIN算法中需要修改这部分
$\succ$ 表示按 TUW 值的升序排列,目的也是用来剪枝。比如在样例中 $a \succ c \succ d \succ b \succ e$
Ps. 存在性质:当一个项集 X,它的 REU(X) = U(X) + RU(X) < minUtil,那么该项集 X 和它的超集全都是低效用项集(反单调性)
$T/X$:$X \subseteq T$,在交易项 T 中大于项集X的所有项集都用T/X表示(因为之前的已经排好序了),例如$T_1 / \lbrace ab\rbrace = \lbrace de\rbrace, T_1 / \lbrace ad\rbrace = \lbrace e\rbrace$,参考上表(枚举树会更容易理解)
每个项集 X 的保留效用(Remaining Utility)$RU(X, T_j) = \sum_{x \in (T_j/X)}U(x, T_j)$
EHIN算法
检索空间
下图枚举树是在以往频繁模式中的原型,但EHIN算法是在该树的基础上进行剪枝操作,需要事先对一元项进行排序操作,
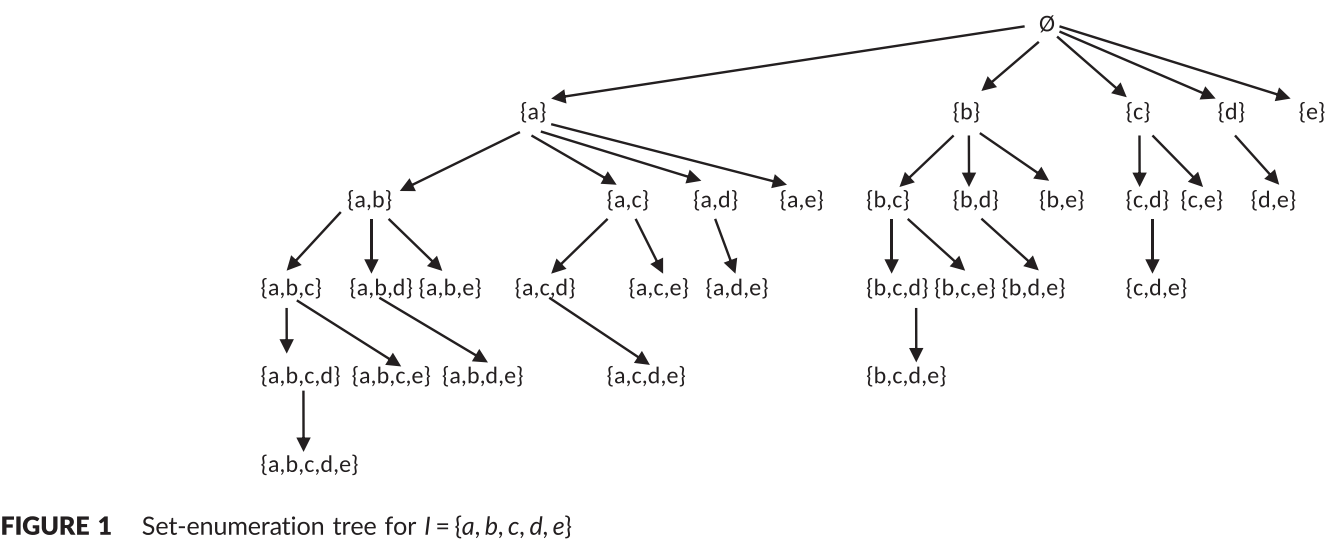
针对负效用
补充定义
- 正效用(Positive Utility)pUtil(X) 是项集 X 的所有正效用值的和,上边界采用该值
负效用(Negative Utility)nUtil(X) 是项集 X 的所有负效用值的和
$E(\alpha) = \lbrace z z \in I \land z \succ x, \forall x \in \alpha\rbrace$,它是所有大于项 α 的所有项组成的扩展项集 - 在剪枝过程中,存在项扩展 Z = α ∪ {w}, 其中 w ∈ 2^E(α) 且 w 不为空(w是枚举树中的修正子树)比如设 α = {b},则 E(α) = {c, d, e},那么一元扩展项集为 {b, c}, {b, d}, {b, e}、多元扩展项集为 {b, c, d}, {b, d, e}, {b, c, e}(可参考上图枚举树)
- 负项的扩展集,同理上条项扩展,但项集 w 只包含负效用
性质
- 项集 X 的效用值 U(X) = pUtil(X) + nUtil(X),其中 pUtil(X) 是该项的正效用值之和,nUtil(X) 是该项的负效用之和,且有 $pUtil(X) \ge U(X) \ge nUtil(X)$
- 根据上一条性质,我们很容易想到要以 pUtil(X) 作为上边界值的预估基准。因为有 pUtil(X) = U(X) - nUtil(X),而nUtil(X) 永远只能降低 项集X 的效用值(因为它永远不大于0)
- 当项集 X 的 U(X) >= minUtil 时,把负效用项(集)加入到该项集 X 中,若组成的新的扩展项集的效用值仍大于 minUtil,那么该扩展项集就是高效用项集(因为扩展负效用项集只会减少原项集的效用值,在减少的情况下仍大于阈值,那么自然也就是高效用项集)
数据库高效扫描
同EFIM算法一样,本算法也是在扫描的过程中计算效用值和上边界值,所以需要在这部分进行操作优化:在进行投影操作之前需要对交易项中的各项元素按RTWU进行排序,其中负效用项排在正效用项后面,再对各交易项按照TU排序,最后才是投影归并操作。
投影策略
依据
当对项集 α 进行深度优先遍历时,不属于 E(α) 的项在计算项集的效用值时会被忽略。
定义
对于 $\forall \alpha$,与它相关的投影交易项(Projected Transaction)被定义为 $\alpha$ - $T$ = $\lbrace i i \in T \land i \in E(\alpha)\rbrace$ 对于 $\forall \alpha$,与它相关的投影数据集(Projected Dataset)被定义为 $\alpha$ - $D$ = $\lbrace \alpha - T T \in D \land \alpha - T \not = \varnothing\rbrace$(也就是依据中讲的那些忽略掉那些不属于E(α)的项后形成的新数据集)。比如设 $\alpha = \lbrace c\rbrace$,那么投影数据集 α-D 包含 $\alpha$ - $T_2$ = $\lbrace e\rbrace$, $\alpha$ - $T_3$ = $\lbrace d, e\rbrace$, $\alpha$ - $T_4$ = $\lbrace d, e\rbrace$, $\alpha$ - $T_6$ = $\lbrace d, e\rbrace$, $\alpha$ - $T_7$ = $\lbrace e\rbrace$
可以参考下图进行理解(下两图中的数据与本文无关):

在原数据集中对项 {c} 进行投影的结果:

交易项归并策略
思路
从上条投影例子中也可以看得出来在对各交易项进行投影之后有项集重复现象,为了减少对数据集的扫描时间和内存消耗,把这些重复的用新的交易项来替代,内部效用直接叠加。
可以结合上两张图,参照下图理解(图中数据与本文无关):

定义
- 当交易项 $T_1$ 与交易项 $T_b$ 的所有包含的项都相同时,称这两个交易项是相同的交易项(Identical transactions)
- 在数据集中存在相同的交易项 $T_{a_1}, T_{a_2}, T_{a_3}, \cdots , T_{a_n}$,用一个新的交易项 $T_M = T_{a_1} = T_{a_2} = \cdots = T_{a_n}$,其中有 $IU(X, T_M) = \sum_{i = 1 \dots n \land X \in T_M}IU(X, T_{a_i})$
- 和项集排序一样,交易项也需要排序,用 $\succ_T$ 表示,规则是从后往前把每个交易项包含的项按照字母顺序对比进行排序。比如有 $T_x = \lbrace a, b, c\rbrace, T_y = \lbrace b ,c\rbrace, T_z = \lbrace a, b, e\rbrace$,那么排序顺序是 $T_z \succ_T T_x \succ_T T_y $
剪枝策略
和EFIM算法一样,并不是基于utility-list的剪枝策略,而是设计一个新的基于sub-tree utility的剪枝策略,使用这些策略的前提是已经把一元低效用项给剪枝并每个交易项和其内部项元素都排好序了。
定义
对 $\forall z \in D$,其修正局部效用值(Redefined Local Utility) \(RLU(\alpha, z) = \sum_{T \in (\alpha \cup \{z\}) \land z \in E(\alpha)}[U(\alpha, T) + RE(\alpha, T)] \\ RE(X, T_c) = \sum_{i \in T_c \land i \succ x \land \forall x \in X}U(i, T_c)\) 比如 α = {a},则 \(RLU(a, b) = [U(a, T_1) + RE(a, T_1)] + [U(a, T_6) + RE(a, T_6)] \\ = [U(a, T_1) + U(b, T_1) + U(d, T_1) + U(e, T_1)] + [U(a, T_6) + U(b, T_6) + U(c, T_6) + U(d, T_6) + U(e, T_6)] \\ = RTU(T_1) + RTU(T_6) \\ = 11 + 17 = 28\) 同理 RLU(a, c) = 17, RLU(a, d) = 28, RLU(a, e) = 28
Ps. 当 $z \in E(\alpha)$,设项 z 可以成为项集 α 的扩展项,有 $z \in Z = \alpha \cup \lbrace z\rbrace, RLU(\alpha, z) \ge U(Z)$;当 RLU(α, z) < minUtil 时,项 z 和所有项集 α 包含项 z 的扩展集都不是高效用集,这些就可以剪掉。
对于 $\forall \alpha \in D, z \in E(\alpha)$,其修正子树效用值(Redefined Subtree Utility) \(RSU(\alpha, z) = \sum_{T_j \in(\alpha \cup \{z\})}[U(\alpha, T_j) + U(z, T_j) + \sum_{i \in T_j \land i \in E(\alpha \cup \{z\})}U(i, T_j)]\) 比如 α = {a},则 RSU(a, c) = (5 + 1 + 2) + (10 + 6 + 11) + (5 + 1 + 20) = 61, RSU(a, d) = 25, RSU(a, e) = 34
Ps. 当 $z \in E(\alpha)$,设项 z 可以成为项集 α 的扩展项,有 $z \in Z = \alpha \cup \lbrace z\rbrace$, $RSU(\alpha, z) \ge U(Z)$,且适用于 Z 的扩展集
设项集 α,有: $Primary(\alpha) = \lbrace z | z \in E(\alpha) \land RSU(\alpha, z) \ge minUtil\rbrace, Secondary(\alpha) = \lbrace z | z \in E(\alpha) \land RLU(\alpha, z) \ge minUtil\rbrace$,且因为有 $RLU(\alpha, z) \ge RSU(\alpha, z)$,所以 $Primaru(\alpha) \subseteq Secondary(\alpha)$
性质
设存在项集 $\alpha、Y = \alpha \cup \lbrace z\rbrace$ 和项 $z$,则存在不等式 $TWU(Y) \ge RLU(\alpha, z) \ge REU(Y)$ = $RSU(\alpha, z)$
计算上边界值
这里个人认为是借助之前的utility-list数据结构思想,使用 Utility Array 首先只要两个简单的循环就可以把上面的 Primary集 和 Secondary集 全部算出来,其次配套使用偏移量可以让后续计算重复使用这个数组结构(跟着代码推一遍也很直观)
利用utility-bin计算$TWU(X)$,有公式 $U[z] = U[z] + TU(T)$,其中 $z \in T$,在处理完最后一个事务时,对于 $\forall i \in I,TWU(i) = U[i]$
下图是个示例:(图中数据和本文无关)

利用utility-bin计算$RSU(\alpha, T_j)$,对于项集 α,
有公式 $U[z] = U[z] + U(\alpha, T_j) + U(z, T_j) + \sum_{i \in T_j \land i \succ z \land i \in E(\alpha \cup z)}U(i, T_j)$,其中 $z \in T_j \land E(\alpha)$,在处理完最后一个事务时,对于 $\forall i \in E(\alpha), U[i] = RSU(\alpha, i)$
利用utility-bin计算$RLU(\alpha, T_j)$,对于项集 α,有公式 $U[z] = U[z] + U(\alpha, T_j) + RU(\alpha, T_j)$,其中 $z \in T_j \land E(\alpha)$,在处理完最后一个事务时,对于 $\forall i \in E(\alpha), U[i] = RU(\alpha, i)$(注意!!!这里算出来的是所有正效用项集的局部效用值)
关键算法
主程序伪代码:

查找正效用项集伪代码:

查找负效用项集伪代码:

个人总结
该算法是在EFIM算法上进行一定程度的修改,定义大多没有什么区别,我自己第一遍看文献的时候觉得和EFIM那篇一模一样,后来在分析代码的时候发现还是有些许不同,比如该算法将负效用的项单独提出来计算。但在个人按照文中给的数据推算过程中,发现部分数据总是对不上,但调试代码发现算法又没有问题,我猜也许是作者手滑写错了吧
参考
- Kuldeep Singh, Harish Kumar Shakya, Abhimanyu Singh, Bhaskar Biswas: Mining of high-utility itemsets with negative utility
