写在前面:本算法为 HUI-Miner 的改进算法,在原有的基础上增加了一些新的数据结构,通过减少生成 utility-list 的数量,进而达到提高运行效率的目的
Faster High-Utility Itemset Mining using Estimated Utility Co-occurrence Pruning
有关算法的绝大部分定义可以直接参考 HUI-Miner,本算法的关注点在于 HUI-Miner 是通过“并”操作实现生成高阶项集的信息,然而,在项的数量较多的情况下,两两相交的操作在检索列表过程中是比较耗费时间,并且对于稠密型数据集,长期维持大量的 utility-list 在内存中也是不小的开支,所以,该算法作者从减少 二阶项集 的数量来在一定程度上解决该问题
Estimated Utility Co-Occurrence Structure
在使用 TWU 的反单调性对所有的 item 进行过滤后,对剩下的 item 进行笛卡尔积运算,形成一个新的元组,即($x$, $y$, $z$={TWU($xy$)})显而易见的是,使用一个矩阵来表示这个元组是最简单的,一方面由于在 HUIM 领域中,项集 $xy$ 是等同于 $yx$,所以该矩阵为左下(右上)三角矩阵。通过再次扫描数据集,可以得到下右表:
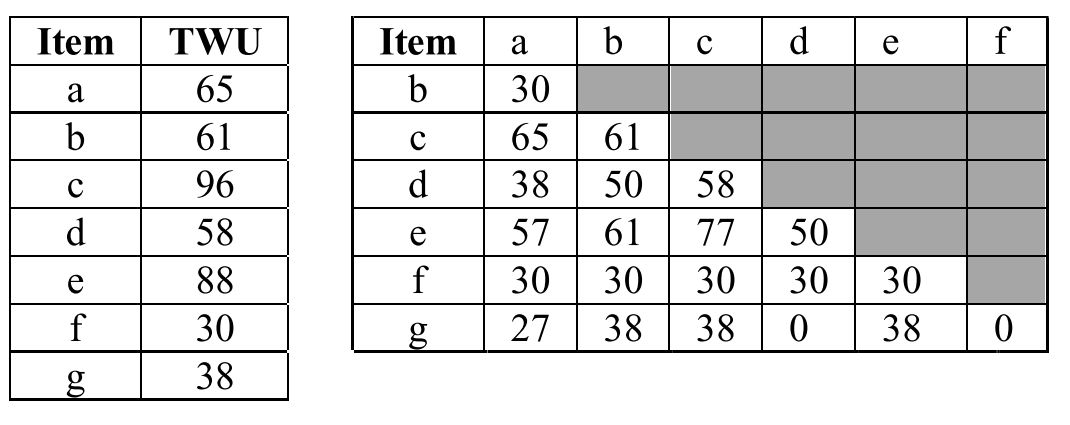
Ps. 当 z 为 0 时,可以不用存储该值
Estimated Utility Co-occurrence Pruning
同样是利用 TWU 的反单调性来进行剪枝,这样可以过滤掉二阶项集
Code
这里使用 HashMap 的嵌套结构来实现 EUCS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
int newTWU = 0;
// 使用列表存储 item
List<Pair> revisedTransaction = new ArrayList<Pair>();
// 对于每一条交易项中的每个 item(items是记录某条交易项中所有 item 的字符型数组)
for (int i = 0; i < items.length; i++) {
// 原数据集中的 item 是字符型,这里转变为整型
Pair pair = new Pair();
pair.item = Integer.parseInt(items[i]);
pair.utility = Integer.parseInt(utilityValues[i]);
// 如果该 item 是 promising
if (mapItemToTWU.get(pair.item) >= minUtility) {
// 记录在 EUCS 中
revisedTransaction.add(pair);
remainingUtility += pair.utility;
newTWU += pair.utility;
}
}
// -------------- 分 -------------- 割 -------------- 线 -------------- //
// 注意区分 mapFMAP(行元素) 和 mapFMAPItem(列元素)
Map<Integer, Integer> mapFMAPItem = mapFMAP.get(pair.item);
if (mapFMAPItem == null) {
mapFMAPItem = new HashMap<Integer, Integer>();
mapFMAP.put(pair.item, mapFMAPItem);
}
for (int j = i + 1; j < revisedTransaction.size(); j++) {
Pair pairAfter = revisedTransaction.get(j);
Integer twuSum = mapFMAPItem.get(pairAfter.item);
if (twuSum == null) {
mapFMAPItem.put(pairAfter.item, newTWU);
} else {
mapFMAPItem.put(pairAfter.item, twuSum + newTWU);
}
}
总结
总的来说,该算法还是比较简单易懂,对 HUI-Miner 算法的整体改进并不大,而且该算法提出的 EUCS 结构仍然存在很大的改进空间(详情可以参考 KHMC 算法)。但是该算法相较于 HUI-Miner 快了将近 6 倍,并且由于减少了无效的二阶项集生成,很大程度上降低了后续不同 utility-list 之间的“交”操作。值得借鉴的是,==EUCS 是一个通用的结构,通过该矩阵是可以大幅度提高 list-based 效用挖掘算法的性能。==
引用
FHM:Faster High-Utility Itemset Mining using Estimated Utility Co-occurrence Pruning