写在前面:FHN算法是基于FHM算法进一步改进得到的,目的也是为了能够计算负效用项,该算法是基于utility-list结构进行合并计算高效用项集。为什么要挖掘负效用项集?举个简单的例子,商家捆绑销售,就单个商品而言是亏损的,但当与利润值高的商品一并销售那么很有可能就是盈利。
An efficient algorithm for mining high-utility itemsets with negative unit profits
样例
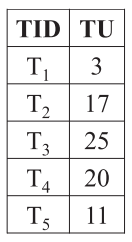
Transaction Dataset:

External Utility of Items:
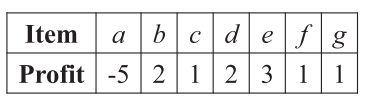
Minimum Utility Threshold:20
Total order of items:$f \succ g \succ d \succ b \succ e \succ a$
定义
大部分定义可以参考 HUI-Miner 算法这篇,现只作一些补充以及关键概念。
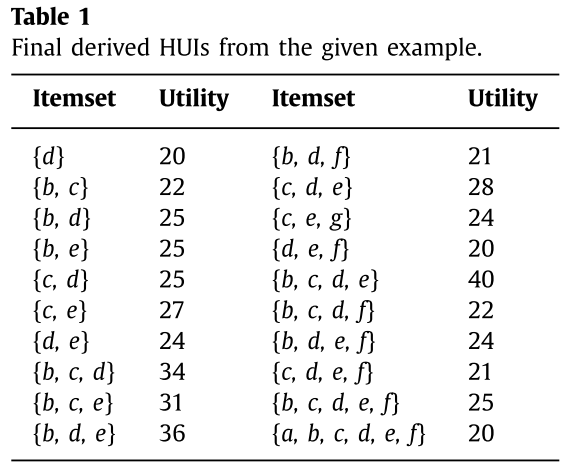
高效用项集(High-Utility Itemset)当项集 $X$ 的效用值大于等于用户设定的阈值,即 $u(X) \ge minUtil$ 时,我们认为该项集是一个高效用项集,应该被输出。下图是本文样例中的所有HUIs:

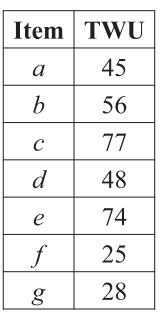
交易项权重效用值(Transaction-weighted utilization)简称“TWU”,提出该概念的主要目的在于解决项集的效用值不具有单调性(monotonic **)或反单调性(anti-monotonic**),所以使用一个权重概念来衡量该项集是否值得进一步挖掘,计算公式如下:$TWU(X) = \sum_{T_{\rm i} \in g(X)} TU(T_{\rm i})$,可以参考下表进行计算验证:


这里补充一下通过 $TWU$ 概念可以得到哪些性质:
- 估值(Overestimation)对于任意的项集 $X$,有 $TWU(X) \ge u(X)$
- 反单调性(Anti-monotonicity)对任意的项集 $X$,其超集 $Y$ 有 $TWU(X) \ge TWU(Y)$
- 剪枝(Pruning)对任意项集 $X$,当 $TWU(X) < minUtil$ 时,$X$ 的所有超集都不可能是高效用项集(参考上一条性质)
修正交易项效用值(Redefined transaction utility)与之前的剩余项集效用值不同,这里重新定义了交易项效用值。计算公式为 $RTU(T_{\rm i}) = \sum_{x \in T_{\rm i} \land p(x) > 0}u(x, T_{\rm i})$ ,即计算交易项效用值过程中忽略所有负效用项。下表显示的是本文中样例计算的TU和RTU结果:

基于正负效用值的概念,有以下几个性质可以使用:
- 设项集 $X$ 在交易项或数据集中,正效用项之和为 $pUtil(X)$,负效用项之和为 $nUtil(X)$,那么其本身得真正效用值为 $u(X) = pUtil(X) + nUtil(X)$,且有 $nUtil(X) \le u(X) \le pUtil(X)$
- 根据上一条说明的关系不等式 $u(X) \le pUtil(X)$,可以把 $pUtil(X)$ 当作上边界值进行估计剪枝界定
- 若使用 $pUtil(X)$ 作为上边界值,那么正\负效用项的扩展项集是不具备向下封闭的性质。举个例子:项集 $X$ 和项 $y$,其中 $y \notin X$,那么显然包含 $X \cup \lbrace y\rbrace$ 的交易项集数量明显是小于或等于包含 $\lbrace X\rbrace$ 的交易项集数量。由于 $y$ 可能是正\负效用项、或者是组合成一个数据集中根本不存在的项集,所以 $pUtil(X)$ > 或 = 或 < $pUtil(X \cup \lbrace y\rbrace)$
- 项集的总效用值之和(Summation of the total utility of an itemset)有以下计算公式:\(SUM(X.iUtil) = SUM(X.pUtil) + SUM(X.nUtil) \\ = \sum_{X \subseteq T_{\rm c} \land T_{\rm c} \in D}X.pUtil(T_{\rm c}) + \sum_{X \subseteq T_{\rm c} \land T_{\rm c} \in D}X.nUtil(T_{\rm c})\)
策略
Positive-and-Negative Utility-list
和 HUI-Miner 一样,利用一元效用项集的utility-list去组合生成2元及以上的效用项集,其中各项之间是有序的
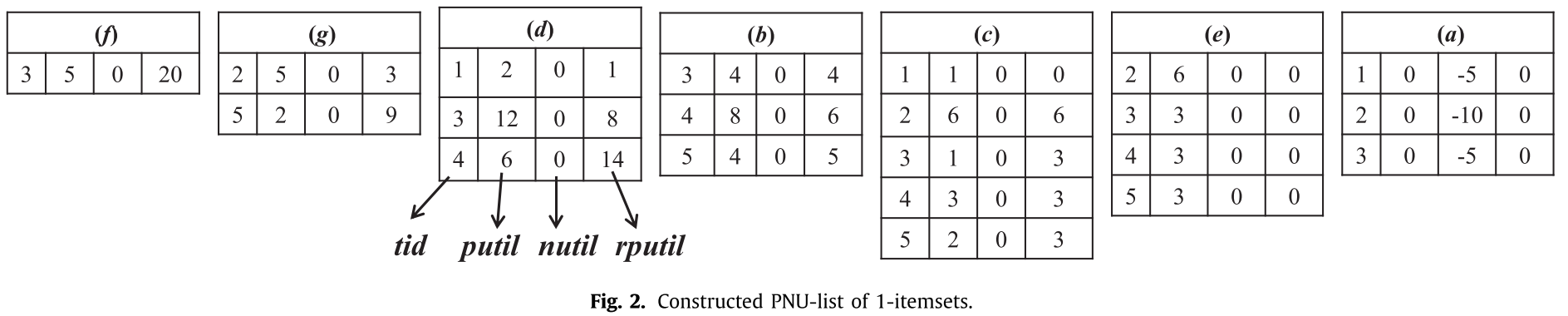
- 正负效用列表(PNU-list)由一个元组组成(tid, pUtil, nUtil, rpUtil),各项解释如下:
- tid:包含项集 $X$ 的交易项编号,以便于后续组合使用
- pUtil:在该交易项中所有正效用项的效用值之和,$\sum_{i \in X \land u(i, T_{\rm tid}) > 0}u(i, T_{\rm tid})$
- nUtil:在该交易项中所有负效用项的效用值之和,$\sum_{i \in X \land u(i, T_{\rm tid}) < 0}u(i, T_{\rm tid})$
- rpUtil:在该交易项中所有剩余效用项的效用值之和,$\sum_{i \in T_{\rm tid} \land u(i, T_{\rm tid}) > 0 \land i \succ x, \forall x \in X}u(i, T_{\rm tid})$
Anti-monotonicity of unpromising itemsets:
利用该性质可以过滤那些不必要的项,在文中已经给出详细证明,即当 $SUM(X, iUtil) < minUtil$ 时,该项集 $X$ 的所有子集都不是高效用项集,可以被剪枝
Estimated Utility Co-occurrence Pruning strategy:
当2元项集不是HTWUI时,那么它的超集自然也不会是HTWUI,可以被剪枝。
LA-Prune strategy:
给定两个项集 $X, \, Y$,当 $SUM(X.pUtil) + SUM(X.rpUtil) - \sum_{\forall T_{\rm c} \in D, X \subseteq T_{\rm c} \land Y \not\subseteq T_{\rm c}}(X.pUtil + X.rpUtil) < minUtil$,那么项集 $\lbrace X, \, Y\rbrace$ 以及项集 $X$ 的拓展集都不会是HUI
算法
PNU-list construct:

可以参考下面的样例结果分析:
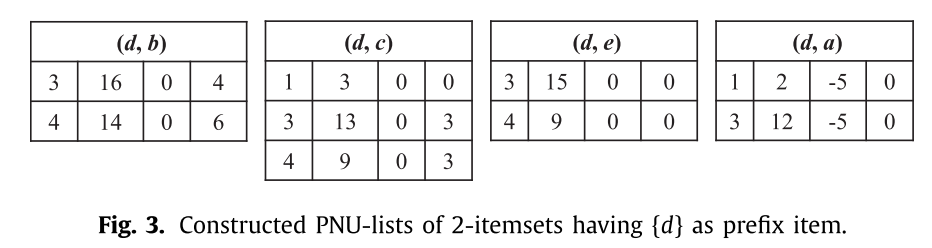
LA-Prune Strategy:

Search procedure:
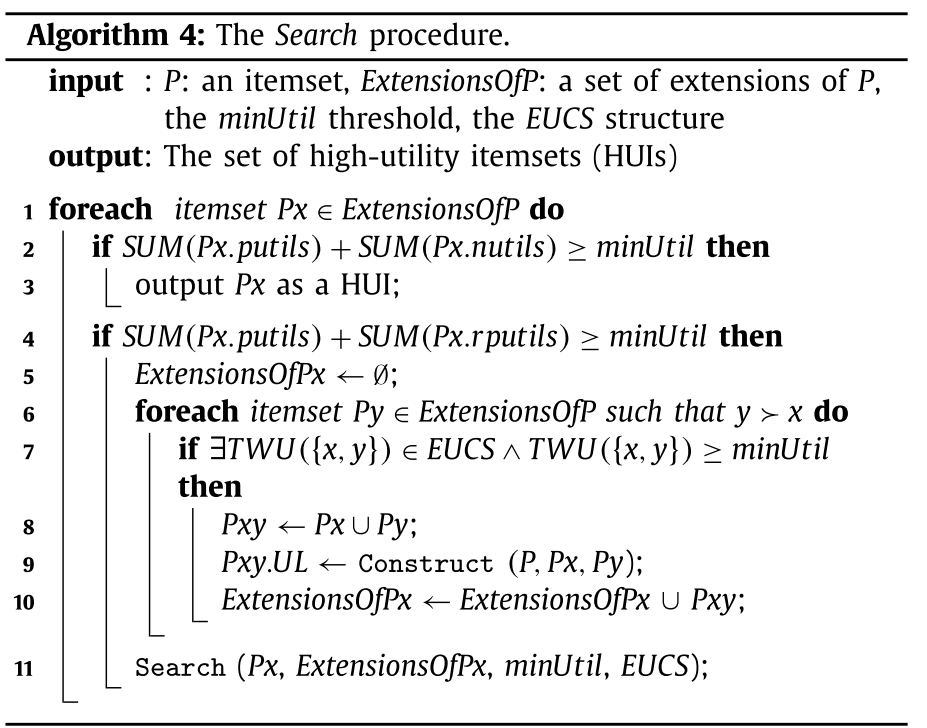
FHN Algorithm:

总结
该算法最精彩的部分在于分别单独提出负效用项和正效用项,对 utility-list 进行了扩充,而且使用多个剪枝策略能够很好地处理庞大的候选集问题(提出了比传统靠TWU来剪枝更紧凑的上边界)虽然相比于后来的EHIN等算法要低效率很多,但在该算法上仍然可以作很多升级。