写在前面:On-Shelf指的是周期性,即冰激凌在冬天销量不高,但夏天卖的很好。每件商品在不同的时期会有不同的销售表现,这就是该领域研究的问题。on-shelf 指代第一个周期、第二个周期、第三个周期…,每个周期之间没有先后顺序,如果一个项集发生在多个周期,那么我们记为 (X, 1),(X, 2)。
FOSHU: Faster On-Shelf High Utility Itemset Mining – with or without Negative Unit Profit
样例
Transaction Database:

External utility of Item:

定义
设项集 $I = \lbrace x_1, x_2, \dots, x_{\rm n}\rbrace$,数据集 $D = \lbrace T_1, T_2, \dots, T_{\rm j}\rbrace$,其中 $T_{\rm i} \in D$ 称为交易项,每个交易项都有一个唯一的编号 $TID$,每个项都有自己唯一的外部效用值 $p(x_{\rm i})$(可以看作是单品利润,可正可负),每个项在不同的交易集中可能有不同的内部效用值 $q(x_{\rm i}, T_{\rm j})$(可以看作是商品购买数量,只能为正数)
特别地,在本论文中,使用 $PE$ 这样的一组正数来作为时间段,每个交易项都关联一个时间段 $pt(T_{\rm j}) \in PE$,意味着在这些时间段内该交易集存在
项(集)效用值(utility of item(set)):在交易项 $T_{\rm j}$ 中,对于项 $x_{\rm i} \in I$,其效用值计算公式为 $u(i, T_{\rm j}) = q(i, T_{\rm j} \times p(i))$;同理,对于项集 $X$,其计算公式为 $u(X, T_{\rm j}) = \sum_{x_{\rm i} \in X \subseteq I \land x_{\rm i} \in T_{\rm j}}u(x_{\rm i}, T_{\rm j})$。效用值可以用来衡量一个物品的重要程度(对商品而言就是利润)
项集的时间段:指的是该商品售卖的时间,定义为 $pi(X) = \lbrace pt(T_{\rm j}) T_{\rm j} \in D \land X \subseteq T_{\rm j}\rbrace$ 在某一时段 $h \in pi(X)$ 内,项集 $X$ 的效用值定义为 $u(X, h = \sum_{h = pi(T_{\rm j})}u(X, T_{\rm j})$,特别地,计算 $X$ 在数据集 -+$D$ 中所有存在时间段的效用值和的公式定义为 $u(X) = \sum_{h \in pi(X)u(X, h)}$
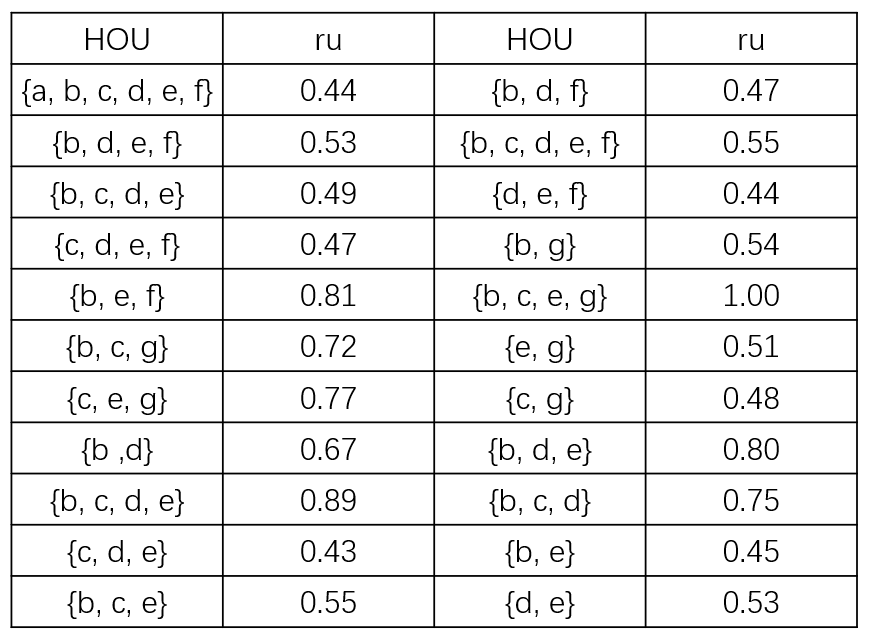
例如:在 Table 1 中我们可以计算项集 $\lbrace c, e\rbrace$ 在周期 1, 2, 3 内均出现,而且在周期2内出现了两次,所以可以得到以下计算过程 $u(\lbrace c, e\rbrace) = u(\lbrace c, e\rbrace, 1) + u(\lbrace c, e\rbrace, 2) + u(\lbrace c, e\rbrace, 2) + u(\lbrace c, e\rbrace, 3)$ = 12 + 2 + 6 + 11 = 31(在周期 2 中存在两个不同的交易项,所以项集计算的效用值不同)
交易项的效用值(transaction utility)交易项内含有许多不同的项,这些项的效用值之和就是该交易项的效用值(TU),TU 可以用来计算各项的 TWU,定义如下:$TU(T_{\rm j}) = \sum_{x_{\rm i} \in T_{\rm j}}u(x_{\rm i}, T_{\rm j})$ 那么针对项集 $X$ 在所有周期内的效用值定义为 $to(X) = \sum_{h \in pi(X) \land h = pt(T_{\rm j})}TU(T_{\rm j})$
其 相对效用值(relative utility)定义为 $ru(X) = u(X) / to(X) $ 当 $to(X) \not = 0$ 相对效用值反应的是该项集产生的利润(损失)占整体的比重,这能指出不同项集的销售业绩,方便零售商在不同时期对货架上的货物进行整理,可以得如下表格: 
high on-shelf utility itemset(HOU):如果一个项集 $X$ 的 $ru(X) \ge minUtil$,其中 $0 \le minUtil \le 1$,设 $minUtil = 0.43$ 时,根据样例我们可以计算得到如下HOUs:

交易项权重效用值(transaction-weighted utilization)和 HUI Mining 一样的问题,需要 $TWU$ 的反单调性来进行裁剪,定义公式为:$TWU(X, h) = \sum_{X \subseteq T_{\rm j} \land h = pt(T_{\rm j})}TU(T_{\rm j})$
一段时间段 $h$ 的效用定义为 $pto(h) = \sum_{h = pt(T_{\rm j})}TU(T_{\rm j})$,那么在此时间段存在的项集 $X$ 的相对效用值定义为:$ru(X, h) = u(X, h) / pto(h)$
- 有 $TWU(X, h) \ge u(X, h)$,故 $TWU$ 可以作为项集在某个时间段的上边界进行提前判定
- $TWU$ 具有反单调性,当项集 $X$ 是项集 $Y$ 的子集时,恒有 $TWU(X, h) \ge TWU(Y, h)$ 成立,即若项集 $X$ 在时间段 $h$ 内不是高效用项集,那么它的子集一定也不是
- 在某个时间段 $h$ 项集 $X$ 的 $TWU$ 除以该时间段的总效用是大于或等于该项集在这个时间段的相对效用值,即:$TWU(X, h) / pto(h) \ge ru(X, h)$
- 当项集 $X$ 不存在时间段 $h$ 有不等式 $TWU(X, h) / pto(h) \ge minUtil$ 成立,那么该项集不可能是HOU,反之,有可能是,需要进一步检查
修正交易项的效用值(redefined transaction utility)同样地,为了解决负效用项的问题,需要重新设计 TU,即 $RTU(T_{\rm j}) = \sum_{x_{\rm i} \in T_{\rm j} \land p(x_{\rm i}) > 0}u(x_{\rm i}, T_{\rm j})$
修正交易项权重效用值(redefined transaction-weighted utilization)同上,项集 X 在时间段 h 上有公式:$RTW(X, h) = \sum_{X \subseteq T_{\rm j} \land h = pt(T_{\rm j})}RTU(T_{\rm j})$
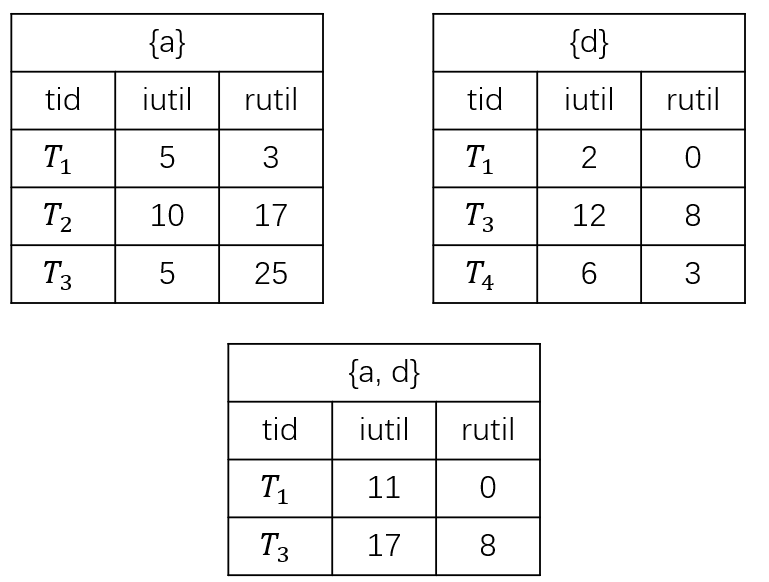
效用列表(utility-list)以项集 $X$ 为核心,记录与该项集相关的信息,而无需再次扫描数据集(Ps. 各项之间依然是有序的 “$\succ$”,具体如何排序根据实际情况而定)。表现形式为 $(tid, iutil, rutil)$,其中 $iutil(X) = u(X, T_{\rm tid})$,$util(X) = \sum_{x_{\rm i} \in T_{\rm tid} \land x_{\rm i} \succ x_{\rm j}, \forall x_{\rm j} \in X}u(x_{\rm i}, T_{\rm tid})$ 可以参考下图示例(注意其各项的计算规则):

- 项集 $X$ 有 $u(X) = \sum_{X \subseteq T_{\rm j}}ituil(X)$
- 项集 $X$ 有 $\sum_{X \subseteq T_{\rm j}}iutil(X) + \sum_{X \subseteq T_{\rm j}}rutil(X) \ge u(X)$,而且该公式比 $TWU(X)$ 更紧凑
针对项集 $X$,在时间段 $h$ 上有 \(sumIUtil(X, h) + sumRUtil(X, h) \ge u(X, h) \\ sumIUtil(X, h) + sumRUtil(X, h) \le TWU(X, h) \\ sumIUtil(X, h) + sumRUtil(X, h) \ge sumIUtil(Y, h) + sumRUtil(Y, h) [X \subset Y] \\ (sumIUtil(X, h) + sumRUtil(X, h)) / pto(h) \ge ru(X, h)\)
在 构造3元及以上utility-list 算法中,设定负效用项永远排序在正效用项后面,且用 $up(X)$ 表示项集 $X$ 内的所有正效用项组成的集合,$un(X)$ 表示项集 $X$ 内的所有负效用项组成的集合,那么有以下性质:
- $u(X, h) \le u(up(X), h)$,因为 $u(X, h)$ 中还可能包含了负效用项的负效用值
- $u(up(X \cup \lbrace z\rbrace), h) \le u(up(X), h)$,和容易想到项集每增加一次长度,能在交易项中出现的次数一定是小于每增加之前的次数
- 当项集 $X$ 不等式 $ru(up(X), h) = u(up(X), h) /pto(h) < minUtil$ 恒成立,且此时只能扩展负效用项,那么该项集及其扩展都不可能为HUO
- 当项集 $X$ 的不等式 $sumIPUtil(X, h) + sumRUtil(X, h) / pto(h) < minUtil$ 恒成立,那么该项集及其扩展都不可能为HUO(其中 $sumIPUtil(X, h) = \sum_{u(X, T_{\rm j}) > 0 \land X \subseteq T_{\rm j} \land h = pt(T_{\rm j})}iputil(X, h)$)
算法
主方法

深度遍历寻找HOUs

构造3元及以上utility-list

总结
这篇算法基于FHM设计,加上FHN处理negative items用到的一些技巧,重点在于理解为什么要讨论on-shelf这种场景,它的应用意义何在。