写在前面：该算法的比较对象是UP-Span，其实我更想知道和UMEpi算法对比两者谁更优劣。因为双方采取的策略和定义优化有很大的相似性，区别在于存储结构的不同。个人认为这篇算法还是比较重要的，关键信息会着重标出。

Fast High Utility Episode Mining

样例

A complex event sequence

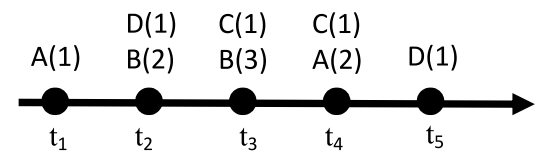
External utility

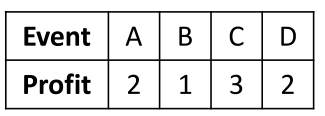
定义

首先我们需要明确什么是”event“？在 Episode Mining 中，event 可以指代一次购物商品记录，也可以是一次风险警告，这里的 event 是广义上的，清楚这一点很重要。理所当然地，每一个event发生都会有一个对应的时间点，时间序列上的每个事件(集)都是处于有序状态，时间维度是 Episode Mining 的必须条件，可以看作是在一个二维坐标系里进行讨论。

• 复杂事件序列（complex event sequence）在简单事件序列（simple event sequence，每一个时间点就只有一个 event 发生，event 前后之间处于有序状态）的基础上进一步扩展，每个时间点上有多个事件同时发生（event set），定义式为 $CES = \big<(tSE_{\rm t_1}, t_1), \ldots, (tSE_{\rm t_{\rm n}}, t_{\rm n})\big>$，其中 $tSE_{\rm t_{\rm k}}$ 指的就是每个时间点上的事件集合，集合长度为 $0 \sim \infty$，样例中的第一个也可以看得出来

• 情节（episode）情节是指一个非空且有多个事件同时发生的有序子序列，表现形式为 $\big<SE_1, \ldots, SE_{\rm k}\big>$，由于事件组合方式不同，每个情节的表示也有点区别，如果两个事件是同时发生，那么我们用 $\big<(AB)\big>$ 表示，如果两个事件是先后发生，那么我们用 $\big<(A), (B)\big>$ 表示，注意区分

• 发生时间段（occurrence）任意情节 $\alpha$ 都会对应的一个或多个时间段（各个事件发生的时间点组成的跨度）$[t_{\rm s}, t_{\rm e}]$ 被称作事件发生。需要明确的是，第一个事件集 $SE_1$ 必须发生在时间点 $t_{\rm s}$，最后一个事件集 $SE_{\rm k}$ 必须发生在时间点 $t_{\rm e}$（这样才是情节发生的时间段，用 $occSet(\alpha)$ 表示）

• 最小发生时间段（minimal occurrence）当情节发生的时间段最小时，我们特别地规定该时间段以便后续计算。例如情节 $\big<(B), (C)\big>$ 发生时间段为 $[t_2, t_3], [t_3, t_4], [t_2, t_4]$（注意事件B和C之是有先后顺序的），其最小时间跨度为1，故 $moSet(\big<(B), (C)\big>) = \lbrace [t_2, t_3], [t_3, t_4] \rbrace$

• 最长时间跨度（maximum time duration）该变量是用户自己设定的一个上限值，因为随着时间跨度不断增长的时候，不仅会增大工作量，而且各个事件之间的联系也会越来越微弱，一个情节的最小发生时间段满足最长时间跨度的要求是 $t_{\rm e} - t_{\rm s} + 1 \le maxDur$

• 事件的效用值（utility of event）这一点和HUIM计算方式一致，即内部效用（quantity，数量）乘以外部效用（profit，利润），涉及到的计算公式（逐步递进）有以下几个：

  • 单个时间点上单个事件的效用值：$u(e, t_{\rm i}) = p(e) \times q(e, t_{\rm i})$
  • 单个时间点上同时发生的事件集的效用值：$u(SE_{\rm k}, t_{\rm i}) = \sum_{\rm j=1}^{\rm l}u(e_{\rm j}, t_{\rm i})$，注意 $SE_{\rm k} = \lbrace e_1, \ldots, e_{\rm l} \rbrace$
  • 最小发生时间段上单个情节的效用值：$u(\alpha, [t_{\rm s}, t_{\rm e}]) = \sum_{\rm i = 1}^{\rm k}u(SE_{\rm i}, t_{\rm n})$，其中 $t_{\rm s} \le t_{\rm n} \le t_{\rm e}$，注意每个事件需要与其时间点一一对应，不在对应时间点上事件的效用值都记为 0
  • 在整个复杂事件序列上单个情节的效用值：$u(\alpha) = \sum_{mo \in moSet(\alpha)}u(\alpha, mo)$

  我们取最后一个效用值计算公式作为例子展示，设 $\alpha = \big< (B), (C) \big>$，那么有 \(u(\alpha) = u(\big< (B), (C) \big>, [t_2, t_3]) + u(\big< (B), (C) \big>, [t_3, t_4]) \\ = [u((B), t_2) + u((C), t_3)] + [u((B), t_3) + u((C), t_4)] \\ = [(1 \times 2) + (3 \times 1)] + [(1 \times 3) + (3 \times 1)] = 11\) 注意 $[t_2, t_4] \not\subseteq moSet(\alpha)$ 且事件 $(B)$ 和 $(C)$ 之间是先后关系不是同时发生

• 高效用情节（high utility episode）当 $u(\alpha) \ge minUtil$ 时，情节 $\alpha$ 就是我们要找的高效用情节（简称”HUE“），挖掘 HUEs 的过程叫做高效用情节挖掘（HUEM）

  论文指出，因为一个情节可以在这个复杂事件序列上有多个存在（因为时间跨度，可以参考 $\big<(A), (B), (A)\big>$），所以之前的HUEM计算只会考虑碰到的第一个情节的效用值，然而实际情况是：不同时间点上相同的事件可能具有不同的内部效用。这样产生的结果就是同一个情节，在不同时间段上产生的效用值大小也不尽相同

针对上面提出的不足，论文对原来的效用值计算方法做出以下修正

• 修正高效用情节（redefined high utility episode）给定两个约束阈值 $minUtil$ 和 $maxDur$，当 $mo \in moSet(\alpha)$，$mo \subseteq maxDur$，$u(\alpha) \ge minUtil$ 时，我们认为情节 $\alpha$ 是 HUE

  • 修正最小发生时间段上单个情节的效用值： \(u(\alpha, [t_{\rm s}, t_{\rm e}]) = u(SE_1, t_{\rm s}) + \sum_{\rm i=2}^{\rm k-1}max\lbrace u(SE_{\rm i}, t_{\rm g(i)x} \mid x \in [1, j]\rbrace + u(SE_{\rm k}, t_{\rm e})\) 可以把整个计算内容分成三段来看：开头，中间最大效用值的组合，结尾。同样以 $\alpha = \big<(A), (B), (A)\big>$ 为例， \(u(\alpha, [t_1, t_4]) = u((A), t_1) + max\lbrace u((B), t_2), u((B), t_3)\rbrace + u((A), t_4) \\ = 2 + max(2, 3) + 4 = 9\)

  • 其它公式计算保持不变

• 并行连接（simultaneous concatenation）在这种连接模式下，拼接后的情节事件跨度不会增加，$simul$-$concat(\alpha, \beta) = \big<SE_1, \ldots, SE_{\rm x} \cup SE_1^\prime, \ldots, SE_{\rm y}^\prime\big>$

• 串行连接（serial concatenation）在这种连接模式下，拼接后的情节事件跨度会增加，$serial$-$concat(\alpha, \beta) = \big<SE_1, \ldots, SE_{\rm x}, SE_1^\prime, \ldots, SE_{\rm y}^\prime\big>$

• 情节权重效用值（episode-weighted utilization）和TWU、SWU类似，作为一个初步筛选的条件，具有向下封闭性（download closure property），在这里讨论的所有情节都必须有 $t_{\rm e} - t_{\rm s} + 1 \le maxDur$，每一个同时发生事件 $SE_{\rm i}$ 都有对应的时间点 $t_{\rm g(i)}$（Ps. 时间点至少有一个），涉及到的计算公式（逐步递进）有以下几个：

  • 在最小发生时间段上单个情节的EWU： \(EWU(\alpha, [t_{\rm s}, t_{\rm e}]) = \sum_{\rm i=1}^{\rm k-1}u(SE_{\rm i}, t_{\rm g(i)} + \sum_{\rm j=t_{\rm e}}^{t_{\rm s}+maxDur-1}u(tSE_{\rm j}, j))\) 其中，$tSE_{\rm j}$ 是指那些不属于 $\alpha$，但在 $\alpha$ 对应的时间跨度内的事件集（可以参照后续举例理解）

  • 在最小发生时间段上单个情节的ERU：与ru、reu相似，$rSE_{\rm t_{\rm e}}$是指在 $t_{\rm e}$ 上除 $\alpha$ 内事件外的其它所有事件组成的剩余事件集，计算公式如下 \(ERU(\alpha, [t_{\rm s}, t_{\rm e}]) = \sum_{\rm i=1}^{\rm k}u(SE_{\rm i}, t_{\rm g(i)}) + u(rSE_{\rm t_{\rm e}}, t_{\rm e}) + \sum_{\rm j=t_{\rm e}+1}^{t_{\rm s}+maxDur-1}u(tSE_{\rm j}, j) \\ u(rSE_{\rm t_{\rm e}}, t_{\rm e}) = \sum_{x \in tSE_{t_{\rm e}} \land x \succ SE_{\rm k}}u(x, t_{\rm e})\)

  • 在复杂事件序列上单个情节的ERU：$ERU(\alpha) = \sum_{mo \in moSet(\alpha)}ERU(\alpha, mo)$

  同样，我们取最后一个来计算作为样例，设 $maxDur = 3$，$\alpha = \big<(A), (D)\big>$，那么有 \(ERU(\alpha) = \lbrace[u((A), t_1) + u((D, t_2))] + u((B), t_2) + u((BC), t_3)\rbrace \\ + \lbrace u((A), t_4) + u((D), t_5)\rbrace \\ = \lbrace [2+2]+0+6 \rbrace + \lbrace 4+2 \rbrace \\ = 16\)

• ERU的反单调性（anti-monotonicity of the ERU）对于待扩展情节 $\alpha$ 和情节 $\beta$，有 $\gamma = simult$-$concat(\alpha, \beta)$ 或 $\gamma = serial$-$concat(\alpha, \beta)$，有规则 $u(\gamma) \le ERU(\gamma) \le ERU(\alpha) \le EWU(\alpha)$ 恒成立，比对它们的计算公式就可以推导出该规则

• （action-Window Utilization of an episode）这是一个比较新颖的计算量，因为 $EWU, ERU$并不能直接运用在复杂事件序列上，所以使用该计算量来筛选候选集 \(\forall mo \in moSet(\alpha), \; mo \subseteq [t_{\rm ei}-maxDur+1, t_{\rm si}+maxDur-1] \\ AWU(\alpha) = \sum_{\rm i=1}^{\rm k}\sum_{j=t_{\rm ei}-maxDur+1}^{t_{\rm si}+maxDur-1}tSE_{\rm j}\) 例如设 $\alpha = (A)$，得 $AWU(\big<(A)\big>) = [0+0+2+4+6]+[4+6+7+2+0]=31$，

  若 $\alpha = (AC)$，得 $AWU(\big<(AC)\big>) = [4+6+7+2+0]=19$（注意这里的 $AC$ 是同时事件集，不是 $A, C$ 序列）

策略

基于AWU的剪枝

利用 $AWU$ 的定义，去替代原来的 $EWU$ 得到长度为一的高效用事件集。因为 $EWU$ 并不是一个很紧凑的上界值，加上计算误差问题（参照定义中的 redefined high utility episode），会产生精度问题

EEUCS structure and EEUCP strategy

如下图所示：EEUCS structure 和 EEUCP strategy 是用来减少 $EWU$ 和 $ERU$ 的计算量

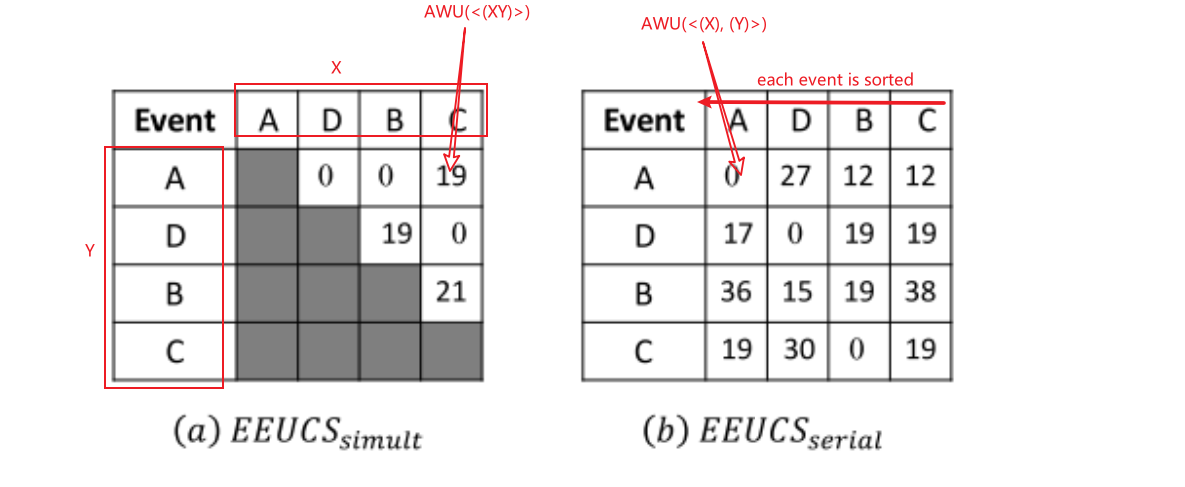
算法

HUE-Span algorithm

MiningSimultHUE algorithm

MiningSerialHUE algorithm

总结

和之前的MEU算法的不同点在于使用了 $AWU$ 作为初步剪枝策略（虽然暂时还没有弄清楚原理，为什么就可以替代），其次是存储结构上的改变，利用矩阵的上下左右延伸很容易得到串行扩展和并行扩展，后续上的拼接方法和以前的算法没有很大的区别。但该算法在剪枝策略上的改变就能得到完整的HUEs，从实验数据上看是很不错的，而且我注意到的是，该算法采用的测试集是transaction database，也就是说把每个tranID当成一个时间点，每一条交易项都是一个同时发生的事件集。