写在前面:距离上一篇USpan算法学习已经过去了很久,这次再来学习 sequence mining,本文解决了关联规则推导这一环节,把以前单纯地挖掘 sequence patterns 的工作推进一步。HUSRM算法运用到的策略比较多,需要花点功夫去研究一下
Efficient Mining of High-Utility Sequential Rules
样例
sequence dataset

utility table
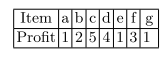
定义
基础定义可以参考 USpan 这篇算法笔记,这里仅作一些内容补充
- 序列规则(sequential rule)设存在两个项集 $X$ 和 $Y$ 有$X, Y \subseteq I$, $X \cap Y = \varnothing$ 和 $X, Y \not= \varnothing$,序列规则 $X \rightarrow Y$ 是相关联的意味着在同一条序列中,项集 $X$ 发生后项集 $Y$ 也会发生,序列规则大小为 $\mid X \mid \times \mid Y \mid$,同时使用 $seq(r)=\lbrace s \mid s \in SDB \land r \subseteq s \rbrace$ 表示包含规则 $r$ 的所有序列,$ant(r)=\lbrace s \mid s \in SDB \land X \subseteq s \rbrace$ 表示包含规则 $r$ 前件的所有序列
- 规则的支持度(support of rule)关联规则 $r$ 在数据集中的支持度同样以比率的形式表现,计算表达式为 $sup_{SDB}(r)=\frac{\mid seq(r) \mid}{\mid SDB \mid}$
- 规则的置信度(confident of rule)关联规则 $r$ 在数据集中的置信度也是以比率的形式表现,计算表达式为 $conf_{SDB} = \frac{\mid seq(r) \mid}{\mid ant(r) \mid}$
- 规则的效用值(utility of a sequential rule)当某条规则 $r: X \rightarrow Y$ 在某条序列 $s_c$ 中存在时,它的效用值计算表达式为 $u(r, s_c) = \sum_{(i \in X \cup Y) \land (r \subseteq s_c)}u(i, s_c)$,如果 $r \not\subseteq s_c$ 时,$u(r, s_c) = 0$;类比推理即可得,该规则在整个数据集中的总效用值为 $u_{SDB}(r) = \sum_{s \in SDB}u(r, s)$
- 高效用序列规则挖掘(high-utility sequential rule mining)给定三个阈值 $minsup$,$minconf$ 和 $minutil$,当某条规则对应的值同时大于阈值,我们认为该规则是高效用序列规则(也就是说约束条件更多了)
挖掘规则需要注意的一点是扩展方式,文中也说明是通过大小为 $1 \times 1$ 的规则逐步左扩展和右扩展得到更长的有趣规则,但需要注意的是左扩展和右扩展先后顺序以及递归方式都会在很大程度上影响最终的挖掘结果;比如规则 $r$:$\lbrace a \rbrace \rightarrow \lbrace c \rbrace$ 既可以先左扩展后右扩展,也可以反过来得到新的规则 $r^\prime$:$\lbrace a, b \rbrace \rightarrow \lbrace c, d \rbrace$,这里就存在生成两条一样新规则的可能;还有一种情况是 $\lbrace b \rbrace \rightarrow \lbrace e \rbrace$ 和 $\lbrace c \rbrace \rightarrow \lbrace e \rbrace$ 都可以分别通过左扩展项 $c$ 和 $b$ 得到同样的新规则 $\lbrace b, c \rbrace \rightarrow \lbrace e \rbrace$,解决办法在下面定义中介绍
扩展(extendability)
左扩展(left extension)对于规则 $X \rightarrow Y$ 和项 $i \in I$ ,当对于 $\forall j \in X$ 有 $i \succ_{lex} j$ 且 $i \not\in Y$,其左扩展为 $X \cup \lbrace i \rbrace \rightarrow Y$
- 右扩展(right extension)同理,当对于 $\forall j \in Y$ 有 $i \succ_{lex} j$ 且 $i \not\in X$,其右扩展为 $X \rightarrow Y \cup \lbrace i \rbrace$
- 需要补充的是,$\succ_{lex}$ 是各个项之间指按字典先后顺序排列(lexicographical),用以解决不同规则因为扩展产生相同的新规则问题;因为一个项有可能既可以左扩展,又可以右扩展,所以通常情况下是默认先左扩展,后右扩展,而且右扩展里可以继续左扩展,但左扩展里只能进行右扩展,用以解决同一条规则因为不同的扩展顺序得到重复的新规则问题
项在序列中的预估值(sequence estimated utility of an item)作用同 TWU,计算表达式为 $SEU(i)$=$\sum_{(s_c \in SDB) \land (\lbrace i \rbrace \subseteq s_c)}SU(s_c)$,其中 $SU$ 是 $s_c$ 序列的总效用值,同 TU,意思是计算在整个数据集中,所有包含项 $i$ 的序列效用值之和;同理,对于由不同项构成的规则 $r$ 的效用预估值也是同样的计算方式 $SEU(r)$=$\sum_{s_c \in seq(r)}SU(s_c)$,这些预估值的作用就是来帮助判断当前的项/规则是否是潜在有趣的,当它们都不小于设定好的 $minutil$,那么我们就认为这些项/规则是可以作进一步扩展,而且很有可能是高效用的
记录效用表格(utility-table)这是单独设计的一个新的存储结构,用来记录所有涉及规则 $r$ 的效用信息,使用 $ut(r)$ 表示(utility-list结构),里面有许多条数据,格式为 $(sid, iutil, lutil, rutil, lrutil)$,其中:
- sid:表示是包含 $r$ 的序列编号($S_{sid} \in seq(r)$)
- iutil:表示 $r$ 在当前序列中的效用值
- lutil:表示那些在当前序列中,可以对 $r$ 进行左扩展的项的效用值之和
- rutil:表示那些在当前序列中,可以对 $r$ 进行右扩展的项的效用值之和
- lrutil:表示那些在当前序列中,可以对 $r$ 进行左/右扩展的效用值之和
后面三个记录扩展的效用值其实都是可以用来作预估值的一部分,方便对 $r$ 进行剪枝,在使用过程中要明确当前进行的是何种扩展方式,把握住扩展项 $i$ 和被扩展项/项集 $j$ 之间的关系就很容易理解;下面继续介绍如何通过utility-table计算扩展规则,给定扩展后规则 $r^\prime$,规则 $r$,扩展项 $i \succ_{lex} j \in s_c$ 以及 $ut(r)$ 和 $ut(r^\prime)$:
- sid:这个必然是前后保持一致,因为扩展规则必须和原规则在同一条序列中
- iutil’:$iutil^\prime(r^\prime)$=$iutil(r)$+$u(\lbrace i \rbrace, s_{sid})$
- lutil’:$lutil^\prime(r^\prime)$=$lutil(r)$-$u(j, s_{sid})$-$u(i, s_{sid})$,其中项 $j$ 不可以成为规则 $r^\prime$ 的左扩展,而是规则 $r$ 的左扩展项,同时项 $i$ 如果可以成为规则 $r$ 的左扩展那么也要减去其效用值,否则无需减去项 $i$ 那部分值
- rutil’:$rutil^\prime(r^\prime)$=$rutil(r)$-$u(j, s_{sid})$-$u(i, s_{sid})$,约束条件同上,只是把左扩展改成右扩展
- lrutil’:$lrutil^\prime(r^\prime)$=$lrutil(r)$-$u(j, s_{sid})$-$u(i, s_{sid})$,其中项 $j$ 不可以成为规则 $r^\prime$ 的左/右扩展,而是规则 $r$ 的左/右扩展,同时项 $i$ 如果可以成为规则 $r$ 的左/右扩展那么也要减去其效用值,否则无需减去项 $i$ 那部分值
之所以需要在扩展后减去项集 $i$ 和 $j$ 的效用值,原因在于关联规则中不可以重复出现同一个项,同时也是避免一个项既右扩展又左扩展
扩展规则的置信度(confidence of extension rule)使用位向量(bit vector)$b(i)$ 来表示项 $i$ 在哪些序列中出现过,使用 $1$ 表示出现,$0$ 表示未出现;然后把项集中的每个项的位向量按位进行与操作,最终$1$的个数就是该项集 $\mid ant(X) \mid$,规则 $r$ 的计算方式也是一样,支持度通过 utility-table 可以直观得到;比如 $bv(a)$=1111 $\land$ $bv(b)$=1011 $\Rightarrow$ $bv(ab)$=1011
Ps. 虽然论文中看起来像是使用一个长长的数组来存储这些0和1,在代码中其实是用hashmap存储相应的键值对,直接通过键的比对计算出新规则的位向量
策略
剪枝策略由于涉及到两个已经研究得很成熟得挖掘领域(frequent 和 utility),分别通过各自的反单调性进行剪枝,只要一个条件不满足我们就删除该节点,不进行下一步的扩展工作, HUI-Miner 这篇笔记有详细的介绍
utility-table
其实utility-list结构存储的信息都是很直观的,因为和该项/项集的所有信息都存储在这个列表当中,我们只需要组合这些已知条件就可以得到关键信息
- 因为会对每个规则 $r$ 单独构造一个list,该list记录了该规则的所有出现情况,所以自然有 $u(r)$=$\sum_{i \in sid}iutil(r_i)$
- 同理,对于规则 $r$ 的支持度计算公式为 $sup_{SDB}(r)$=$\frac{\mid ut(r) \mid}{\mid SDB \mid}$
- $iutil(r)$+$rutil(r)$+$lutil(r)$+$lrutil(r) \le SEU(r)$,故utility-table其实是提供了一个更紧凑的边界值(预估值,把公式细化就可以推导出)
- 若规则 $r$ 经过一次左/右扩展得到新的规则 $t$,有 $u(t) \le iutil(r)$+$rutil(r)$+$lutil(r)$+$lrutil(r)$ (因为每进行一次扩展,包含这条新规则的序列就更少了)
- 若规则 $r$ 经过一次左扩展得到新的规则 $t$,有 $u(t) \le iutil(r)$+$lutil(r)$+$lrutil(r)$
compact utility-table
作者在实验过程中观察到两条规律:
在左扩展过程中:
- $rutil$ 总是用不到的,所以可以不用计算该值
- $lutil$ 和 $lrutil$ 之和一直都需要使用,所以可以用它们的和来替代这两个数值
显然,这会让table变得更小,而且构造所需要的时间也会短一些
在任意一条序列中,排在某规则第一次出现位置之后的项可以作为右扩展,对应地,排在之前的可以作为左扩展
算法
HUSRM algorithm

Left Expension

Right Expension

总结
以上就是HUSRM算法的全部内容,借鉴了utility-list思想,直接通过list而不用遍历数据集构造更高阶层的规则,也是高效用序列规则挖掘领域的一个突破性工作。个人认为作者将原算法拆出了四个不同程度优化的版本来进行实验比对,这是非常有趣的地方,其实我们不妨揣摩一下作者这么安排的用意。这类算法的最大问题在于运行时间过长,因为复杂的构造过程,很多算法的实验效果并不是很好看,还需要多加研究,是否有一个更高效的存储结构来简化构造过程,或者新的构造思路。