写在前面:处理现实的数据集(即时刻变化中),如何在这些动态数据集上或者对两个不同时刻的同一数据集进行挖掘分析是一个很有价值的问题;因此,该论文提出了一个新的概念叫做 emerging pattern 来表示那些支持度显著变化的项,并以此设计了一种更高效的分类算法
Efficient Mining of Emerging Patterns: Discovering Trends and Differences
动机
在时态数据库中,通常是为了研究项集的变化情况:如在金融领域,通过分析项集的变化情况可以进行趋势预测;又如对比不同类别的项的变化情况,可以进行比对分析;或者是在总量基数过大的情况下,在总数据量占比上变化不明显,但实际数值变化很大等这类数据分析情况。根据以上需求,本文提出 emerging pattern(EP)来量化描述这些变化情况
定义
项(item):数据集中的最小单位,不可再分割,用 $x_i$ 表示
项集(itemset):由多个不同的项构成,用 $X$ 表示,其中 $k$-$itemset$ 表示该项集包含 $k$ 个项
超大/小项集(large/small itemset):给定一个最低支持度阈值 $\sigma$(百分比形式),如果 $supp_\mathcal{D}(X)$ = $\frac{count_\mathcal{D}(X)}{\mid \mathcal{D} \mid} \ge \sigma$,那么用 $Large_\sigma(\mathcal{D})$ 表示在 $\mathcal{D}$ 中所有符合该不等式的项集的集合,反之是 $Small_\sigma(\mathcal{D})$
闭区间(interval closed):区间内任何元素都不小于左边界且不大于有边界,而 $Large_\sigma(\mathcal{D})$ 就是一个闭区间
交易项(transaction):由多个不同的项构成,可以划分成多个项集,用 $T$ 表示
支持度(support):衡量一个项/项集是否为用户需要的一个量化指标,计算公式为 $supp_\mathcal{D}$ = $\frac{count_\mathcal{D}(X)}{\mid \mathcal{D} \mid}$,其中分子表示 $X$ 在数据集 $\mathcal{D}$ 中总共出现的次数,分母表示该数据集包含多少条交易项;本论文使用支持度的变化率(GrowthRate)来衡量一个项/项集是否是需要的
- 当 $supp_1(X)$ = 0 且 $supp_2(X)$ = 0,则 $GrowthRate(X)$ = 0;
- 当 $supp_1(X)$ = 0 且 $supp_2(X) \not=$ 0,则 $GrowthRate(X)$ = $\infty$;
- 否则,$GrowthRate(X)$ = $\frac{supp_2(X)}{supp_1(X)}$
其中,$supp_1(X)$ 和 $supp_2(X)$ 分别是 $X$ 在原数据集 $\mathcal{D}_1$ 和发生变化的数据集 $\mathcal{D}_2$ 中的支持度,且 $\mathcal{D}_2$ 在排序上后于 $\mathcal{D}_1$
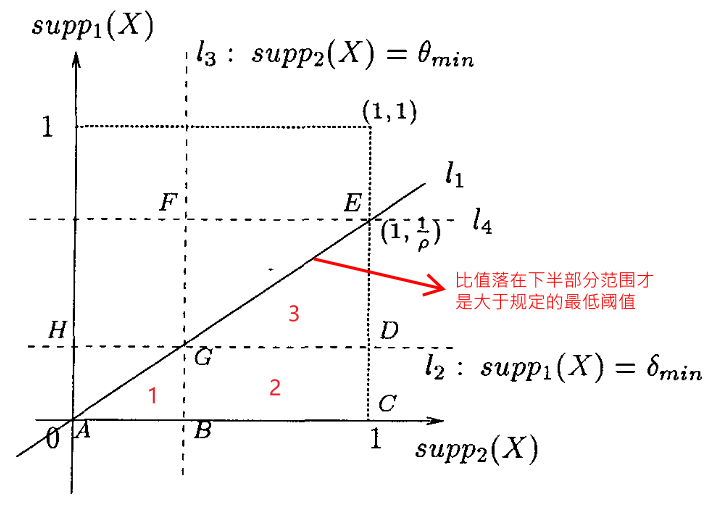
因为该算法考虑的是变化率,所以用二维坐标来描述问题会更直观,如下图,

根据 $l_1$,$l_2$ 和 $l_3$ 三个条件可以得到 1,2 和 3 等三个挖掘 EP 的区间,
- 区间 1:同时低于两个预设的阈值,意味着该项在整体的占比很小,但是前后变化很大的情况,遗憾的是目前没有好的办法解决该情况
- 区间 2:本论文主要研究的对象,通过前后两个数据集中的最大项集作为边界来约束检索空间(即 长方形$BCDG$),进而达到快速且精准地挖掘所有的 EP;比如某商品销售量暴增
- 区间 3:同时大于两个预设地阈值,意味着该项的基数很大,仅通过数值是无法明显观察出变化情况,需要用比率的形式来凸显
边界(border):形如 <$\mathcal{L}$, $\mathcal{R}$> 这样的有序对被称为边界,其中 $\mathcal{L}$ 是左边界,$\mathcal{R}$ 是右边界(Ps. 注意,这两个边界都是集合,并不是一个数值,所以他们又可以分别看成是 最小集 和 最大集 );因此,闭区间 [$\mathcal{L}$, $\mathcal{R}$] 的边界是 <$\mathcal{L}$, $\mathcal{R}$>
- 同理,超大/小项集也可以成为边界,分别用 $LargerBorder_\sigma(\mathcal{D})$ 和 $SmallBorder_\sigma(\mathcal{D})$ 表示
- 其次,在数据集中,$SmallBorder_\sigma(\mathcal{D})$ 必然是 空集(不能有更小的边界存在),为此要找出所有的 EP 只要明确 $LargerBorder_\sigma(\mathcal{D})$ 即可
算法
Border-Diff
该过程主要是为了利用一对边界之间的差异推导出一个新的边界

额外说明一下 “non-minimal itemsets”:由原文可知,基础版本的 Border-Diff 第一步结束后,$\mathcal{L}$ = {{1}, {1, 4}, {1, 3}, {1, 3, 4}, {1, 2}, {1, 2, 4}, {1, 2, 3}, {2, 3, 4}}(注意是按照枚举顺序来写的);第二步需要移除的是超集(也就是 non-minimal itemsets ),保留最小子集(超集可以通过子集枚举树扩展得到);因此最后得到的 $\mathcal{L}$ = {{1}, {2, 3, 4}}
MBD-LLBorder

总结
该论文是上个世纪发表的文章,但清晰地解释了何为 emerging pattern 以及为什么要挖掘这种对象;全文用到了大量的数学公式和证明过程,可以说是进入该领域内需要掌握的一篇基础论文。该论文主要是为了构造分类器提出新的算法,而在效用领域是否也可以使用这个概念呢?还需要更多研究,从检索结果来看并没有很多学者在推进这方面的研究,可以先看看他们的工作成果,尝试着结合项集效用挖掘