写在前面:传统的 top-$k$ 查询是针对事务的某个维度进行考量,比如找出利润最高的 $k$ 个商品组合,最频繁出现的 $k$ 个网络攻击等等。不可置否,这些单一查询是非常高效且有用,但在大多情况下,由于事务的复杂性,制定策略需要考虑多个维度。比如去某地旅游,预定的旅馆是综合考虑价格和距离景区的结果。因此,本文介绍如何在静态交易数据集上使用 Skyline 查询
Mining of skyline patterns by considering both frequent and utility constraints
动机
top-$k$ 查询结果过于单一(过于片面强调某一个维度),skyline 查询中视所有维度是同等重要的,得到的是综合考量的结果
定义
频繁度(frequency)和效用值(utility)相关定义请参考 HUI-Miner 笔记
skyline:指的是一组点的集合,即除去这个集合,在整个数据集中不存在比这些集合中的点更优的情况
dominate:在数据集中,项集 $X$ 优于另一个项集 $Y$ 的条件是 $f(X) \ge f(Y)$ 且 $u(X) > u(Y)$ 或者 $f(X) > f(Y)$ 且 $u(X) \ge u(Y)$,通常用 $X \succ Y$ 表示
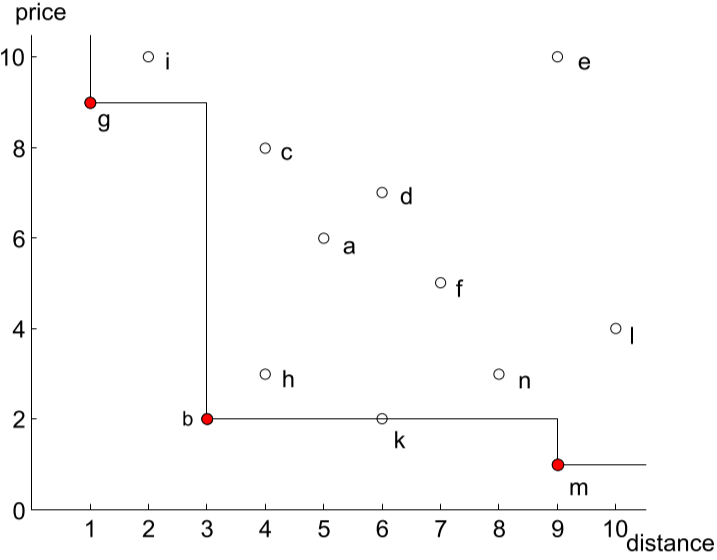
SFUP:当某个项集 $X$ 在数据集中不存任何的项集都优于它,那么 $X$ 被视为 skyline frequent-utility pattern,如下图所示,项 $g$,$b$ 和 $m$ 都是 SFUP

utilmax:当最大效用值的项的频繁度大于或等于存入位置的索引值(Ps. 其实就是频繁度),公式为 $utilmax(i) = max{u(X) f(x) \ge i}$。本质上,该结构可以看成是一个定长的数组,类似于把上图进行扁平化(二维变成一维,索引表示 x 轴上的刻度,存入的值表示该点对应 y 轴上的值)、 这样做的好处显而易见,先确保频繁度是一定不低于的情况下,再专注于考虑效用值的大小情况,简化了判断流程
策略
根据 utilmax 结构,当一个项集 $X$ 在数据集中的效用值小于 $utilmax(f(X))$,那么该项集一定不是 SFUP,证明过程如下: \(\begin{array}{l} 设存在两个项集 X 和 Y 有 f(Y) \ge f(X),且 u(Y) = utilmax(f(X)) \\ \because \sum_{X \subseteq T_q \land T_q \in \mathcal{D}}u(X, T_q) < utilmax(f(X)) \\ \therefore u(X) < u(Y). \\ 又 \because f(Y) \ge f(X) \\ \therefore Y 优于 (dominate) X,X 不是 SFUP. \end{array}\)
根据 utilmax 结构,当一个项集 $X$,其在数据集中的总效用值和剩余效用值之和仍然小于 $utilmax(f(X))$,那么该项集的所有超集一定都不是 SFUP,证明过程如下: $$ \begin{array}{l} 给定项集 X 和其超集 X^\prime (X \subseteq X^\prime),对 \forall T_q (交易项集) \supseteq X^\prime 有 (X^\prime - X) = (X^\prime / X)
\because 由 X \subset X^\prime \subseteq T_q 可得 (X^\prime/X) \subseteq (T_q / X),
\therefore f(X^\prime) \le f(X)
且u(X^\prime, T_q) = u(X, T_1) + u(X^\prime-X, T_q)
= u(X, T_q) + u(X^\prime / X, T_q)
= u(X, T_q) + \sum_{i_j \in X^\prime / X}u(i_j, T_q)
\le u(X, T_q) + \sum_{i_j \in T_q / X}u(i_j, T_q)
= u(X, T_q) + rutil(X, T_q). \\because 由 X \subset X^\prime 可得包含 X^\prime 的交易项集的数量必然是小于或等于包含 X 的交易项集\的数量,即 tid(X^\prime) \subseteq tid(X)
\therefore u(X^\prime) = \sum_{T_q \in tid(X^\prime)}u(X^\prime, T_q)
\le \sum_{T_p \in tid(X^\prime)}[u(X, T_p) + rutil(X, T_p)]
\le \sum_{T_p \in tid(X)}[u(X, T_p) + rutil(X, T_p)]
< utilmax(f(X)). \又 \because f(X^\prime) \le f(X)
\therefore \exists Y 有 f(Y) \ge f(X) \ge f(X^\prime) 且 u(Y) = utilmax(f(X)) \ge u(X^\prime).
得证 X^\prime 必然不是 SFUP.
\end{array} $$ 其中 $rutil(X, T_q)$ 表示项集 $X$ 在交易项集 $T_q$ 中的剩余效用值大小
伪代码
这篇论文借用效用列表(utility-list)数据结构,提出了基于深度遍历和基于广度遍历的两种检索算法,但个人认为核心点在于 Judge 过程,其它伪代码可以直接参考原文或 HUI-Miner 笔记
Judge pseudo-code

总结
Skyline 查询的优势相较于 top-$k$ 查询是显而易见的,考虑多个维度得到的结果更具备可解释性,也更加贴近事实特征。但是该方法只适合查询具备单调线性变化的维度,如果是曲线变化那么在判断上会有更高的要求。utilmax 数据结构在该算法中是非常关键的,通过该一维数组来判断某个点是否为边际点是非常直接且高效。当然,在该算法中,utilmax本身还是过长(大小为数据集的交易项总个数),实际上可以调整为在整个数据集中的最大频繁度即可