写在前面:SPADE在序列挖掘中属于比较早且有名的算法,针对序列挖掘任务本身的一系列痛点给出了一套解决方案,如 栅格检索(lattice search technique),id列表(vertical id-list)等等。之前研究的情节效用(episode utility)也属于序列挖掘下的一个分支,区别在于SPADE考虑每条序列是互相独立状态,而episode sequence是相互关联。虽然该算法的性能并不如当前那么好,但是其设计思路仍然可以学习一下
An Efficient Algorithm for Mining Frequent Sequences
介绍
人们的一连串行为可以看成一个个序列(互相之间即可独立也可关联,出于简化问题,本文只考虑独立关系);每个序列(sequence)又可以分割成几个步骤(event),不同步骤之间既可以是先后(serial)执行,也可以是同时(parallel)执行;每个步骤还可以进一步细分成具体的行动(item),这些行动也是有先后顺序(主体只有一个人,默认不存在同时行动),由于在算法中采用的是符号化,所以每个item之间的排序规则设置为 词典序列(lexicographic order)。出于方便考虑,SPADE算法默认同一条sequence中不会出现多个events同时发生(区别于episode),如下图所示:
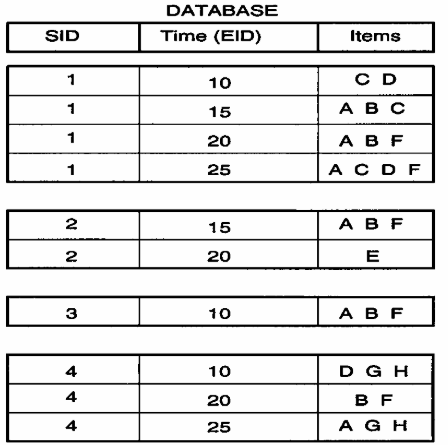
解决问题
- 挖掘频繁的子序列,如从 $D \rightarrow {BF} \rightarrow A$ 得到 ${BF}$;
- 挖掘有跨度的子序列,如从 $D \rightarrow {BF} \rightarrow A$ 得到 $D \rightarrow {BF}$;
- 挖掘对象具有很高的一般性,可以直接适用于 categorical sequential domain,如DNA序列、文本分析、网页行为分析等等
策略
格论(lattice theory)
令集合 $P = {X, Y, Z}$,有以下偏序关系成立:
- 自反性:$X \le X$
- 对称性:$X \le Y$ 且 $Y \le X$ 则 $X = Y$
- 传递性:$X \le Y$ 且 $Y \le Z$ 则 $X \le Z$
设集合 $S \subseteq P$,当 $X$ 是 $S$ 的上/下边界时(upper/lower bound),对 $S$ 进行 并($\lor$)/ 交($\land$)可以得到上确界(最小,minimum upper bound)/下确界(最大,maximum lower bound);当集合 $L$ 中的任意两个元素都有上确界和下确界,那么 $L$ 被称为 格(lattice),同样 $L$ 的 子格(sub-lattice)也必须符合上述条件;更进一步,当 $X \land Y$/$X \lor Y$ 表示的是一组上/下确界集合,那么 $L$ 被称为 超格(hyper-lattice)
Ps. 需要注意的是,在本文中作者研究对象是超格,但是用格来指代,请不要混淆
向下闭合性(download-closure property)
在没有约束的情况下,序列可以产生无限个子序列组合(也就是说这个格是无限大),所以根据实际情况,限定了一个序列中最多有 $C$ 个 events,每个 event 最多包括 $T$ 个 items,即序列最长为 $C · T$。设给定序列 $X$ 和 $Y$ 都是频繁的,那么它们两两相交运算称为 交-半格(meet-semilattice),同理,两两相并的运算称为 并-半格(join-semilattice)(Ps. 详细的“半格”概念请参考离散数学介绍的内容)。而 交-半格 具备 闭包性(closed),故当 $X$ 和 $Y$ 是频繁的,可以推得 $X \land Y$ 也是频繁的(最大下界);反之 $X \lor Y$ 并不成立(最小上界)。由此可以得到一个非常有名的剪枝策略,频繁集合不存在非频繁的子集,当某个检测到某个子集是非频繁的,那么在后续检测过程中可以跳过所有包含该子集的集合
交运算计数
论文中提到一种计算支持度的方法,通过给每个元素构造一张id列表,该列表记录的形式为 (sequence’s id, event’ s id)这两个参数可以直接定位改元素在数据集中的位置,如下图所示: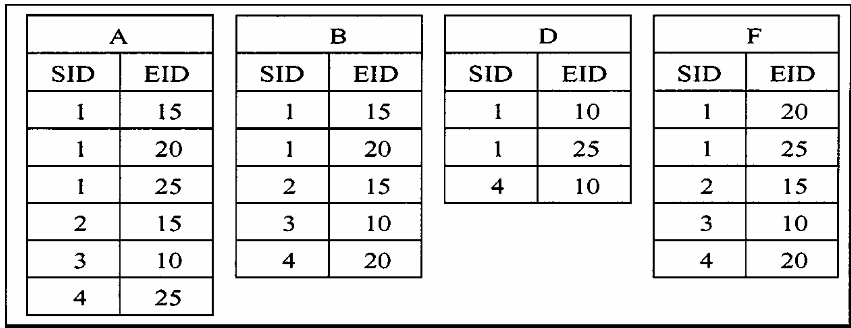
通过 交运算 来得到两个元素构造高阶集合的支持度,首先是以 sequence’s id 为基础的 temporal join ,然后是以 event’s id 为基础的 equality join,这样就能够得到该高阶集合出现位置的完整信息
分治思想
论文中讲到序列挖掘费时费内存(长度为k的sequence的时间复杂度为 O($n^k$)),因此使用了一种策略,将大的任务切块成各个独立的小任务。该算法采用共同前缀思想,把具有相同前缀的集合放在一起处理,而且划分方法可以共同前缀的长度来定,如下图所示: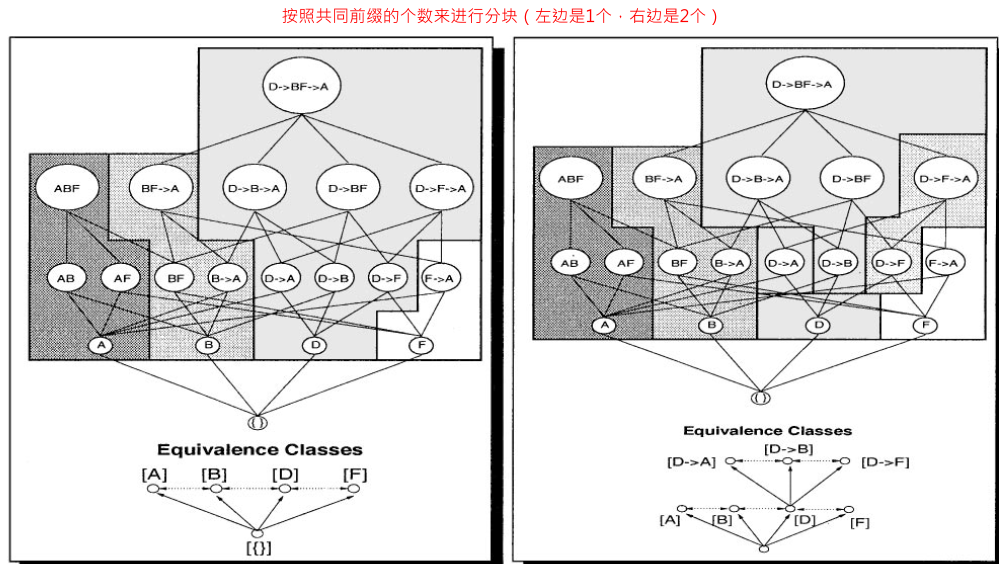
而且文中借这种方法,对 深度优先遍历(Depth-First Search, DFS) 和 广度优先遍历(Breadth-First Search, BFS) 两种检索策略进行了探讨。如 BFS 优势在于比 DFS 提前知道更多的信息,可以辅助后续生成高阶集合的剪枝过程;由于 DFS 只是在单枝上进行挖掘,所以在内存中保存的信息具有连贯性,可以节省大量的内存资源(Ps. 就这一点而言,大多数挖掘算法偏向于采用 DFS 策略)
伪代码
需要指出的是,SPADE算法并没有采用和Apriori、FP-Growth算法一样处理的 horizontal database,而是选择 vertical database
Main algorithm

Searching space

Ps. 这里涉及到如何避免不同元素组成的集合出现重复的情况,可以参考之前 HUSRM算法笔记 中介绍到的几种构造思路
总结
由于SPADE算法发表得比较早,所以分析代码并不复杂,个人认为这篇论文的亮点在于花了很长的篇幅讲清楚频度挖掘的原理,是不可多得的文献,作为初学者可以细细研究一番,如 格的概念是整个挖掘算法的核心,而且为了简化格的运算,对深度优先遍历和广度优先遍历方法也进行了不同程度的优化,提前剪去不必要的节点。另外,如果阅读近些年发表的相关领域论文,挖掘不一定得从下往上,根据数据集自身特点进行自上而下的挖掘思路在性能方面表现也是不错的.