写在前面:根据传统的效用项集挖掘算法得到的高效用项集,是一个高度抽象的集合,并没有反应出该集合内部元素为什么能够构成高效用项集,它们之间存在何种关联也无从得知,因此,cross-level HUIM algorithms正是为了解决该问题而提出
Mining Top-K Cross-Level High Utility Itemsets
定义
大部效用值计算分内容在 HUI-Miner、kHMC 算法笔记中已经有介绍,这里仅做一点额外补充
分类(taxonomy):是一棵树($\tau$),叶节点表示具体的项,父节点表示分类标准(不同程度的抽象)
广义项(generalized item):表示一个高层次的抽象,如波斯猫和老虎都可以归类为猫科动物,简写为 $GI$;由此引申出一个概念 局部关系(location relationship),即在 $\tau$ 中,存在一条路径从节点 $g$ 到节点 $i$,有 $(g, i) \in LR \subseteq GI \times I$
抽象项(abstract item):是非广义的,简写为 $AI$ = $GI \cup I$($I$ 是项集合);同理引申出一个概念 泛化关系(generalization relationship),即在 $\tau$ 中,存在一条路径从节点 $d$ 到节点 $f$,有 $(d, f) \in GR \subseteq AI \times AI$
具象化(specialization):从某个广义项 $g$ 节点出发,沿着树枝走到叶节点,称为对 $g$ 进行特殊化,公式为 $Leaf(g, \tau)$ = {$i \mid (g, \tau) \in LR$};当项集 $X$、$Y$ 有 $\forall f \in X$,$f \in Y$ 或 $\exists d \in Y$ 有 $f \in Desc(d, \tau)$ 且 $\mid X \mid$ = $\mid Y \mid$,则称 $X$ 是 $Y$ 的具象化项集
衍生(descendant):自然地, $g$ 的所有子节点公式化为 $Desc(g, \tau)$ = {$f \mid (g, f) \in GR$};当项集 $X$ 和 $Y$ 有 $\forall f \in X$,$\exists d \in Y$ 有 $f \in Desc(d, \tau)$ 且 $\mid X \mid$ = $\mid Y \mid$,则称 $X$ 是 $Y$ 的衍生项集
cross-level pattern:同时包含广义项和抽象项
multi-level pattern:针对不同的抽象层次,设置不同的阈值,多层筛选后得到的 cross-level patterns
generalized-weighted utilization:与 $TWU$ 功能类似,有反单调性的特点,计算公式为 $GWU(X)$ = $\sum_{T_i \in g(X)}TU(T_i)$,其中 $g(X)$ 是指包含项集 $X$ 的交易项集合
偏序关系($\succ$):对于 $AI$ 中的所有项,存在一种排序规则,即当 $level(a) < level(b)$ 或者 $level(a) == level(b)$,$GWU(a) < GWU(b)$ 时,则有 $a \prec b$
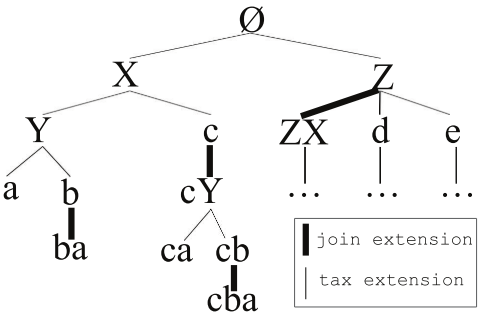
基于并操作的扩展(join-based extensions):对于项集 $X$,jion-based extension 是将项 $y \in AI$ 直接加入 $X$,同时条件 $i \prec y$ 且 $\forall i \in X$,$y \not\in Desc(i, \tau)$ 要成立
基于分类的扩展(tax-based extensions):将项集 $X$ 当前最后一个项 $y$ 替换为 $X$ 的其它子节点叫做 tax-based extensions
Ps. 两种扩展方法示意图如下:

分类效用列表(tax-utility-list):基于 utility-list 结构改进的新存储结构,相较于原来添加了分类信息,即 $tuList(X)$ = <$(tid, iutil, rutil)$,$children$>,其中 $children$ 记录项集 $X$ 中最后一个项的所有子节点对应的 $tuList$
Ps. tuList 结构示意图如下:

动机
销售中的产品可以分成多个大类(广义上)如面包、牛奶等等,而在这些大类中又可以分成多个小类(垂直细分),如白面包、燕麦面包、荞麦面包等等。传统的 HUIM 算法只能分析出广义上的集合,即结果显示 “牛奶+面包” 可以销售得很好,而不能得出具体是 “哪种面包+牛奶” 卖得好(Ps. 如果把挖掘对象分得太细,传统的 HUIM 算法可能会因为低于阈值而过滤了某些结果)。其次,人为设置阈值很难保证短时间内得到满意的结果(阈值偏大或偏小会严重影响挖掘结果),所以使用 Top-$k$ 思想来转换获取结果的思路,避免这个问题
策略
基于反单调性的剪枝策略
该策略在效用挖掘中是通用的存在,当 $GWU(X) < minUtil$ 时,项集 $X$ 本身及其扩展都不可能成为符合条件的高效用项集
基于剩余效用的剪枝策略
该策略在基于utility-list数据结构的算法中最容易实现,也最符合list结构的特点,当 $reu(X)$ = $\sum_{e \in tuList(X)}(e.iutil + e.rutil)< minUtil$ 时,项集 $X$ 和它的扩展项集都不可能是高效用项集
基于广义项的效用阈值提升策略
在挖掘开始前的准备工作中,找出 $GWU > minUtil$ 的一阶项,而这些低阶项的真正效用值可以用来提升当前的最低阈值
伪代码
该算法是基于 CLH-Miner 算法改进的 Top-$k$ 版本,通过深度优先遍历方式,采用 join-based 和 tax-based 两种扩展方式挖掘高阶高效用项集
Main procedure

Find procedure

由于原论文中并没有提供实现 construct join-based extensions,construct tax-based extensions 和 construct() 的伪代码,所以本人从 CLH-Miner 和 HUI-Miner 算法中截取对应的伪代码
ConstructJoinExtension procedure

ConstructTaxExtension procedure
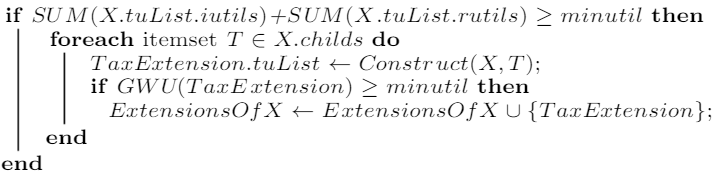
Construct procedure

总结
由于该文章是与其基准算法 CLH-Miner 是同一年发表的,所以在阈值提升策略上并没有做很好的优化,只是采用了一些 top-$k$ HUIM 算法中比较通用的策略。但该算法是首个能解决 top-$k$ cross level HUIM 问题。从实验结果来看,该算法在时间上表现比较好,但是在内存上随着 $k$ 值的增大而急剧增加,这是 utility-list 数据结构的一个通病。个人认为应该在数据结构上进行改进,使用压缩程度更高的来提高挖掘效率,减少无效candidates的产生