写在前面：模糊效用（fuzzy utility）挖掘和不确定数据集（uncertain dataset）之间有什么区别吗？两者又是不是能够结合在一起使用呢？今天要记录的这篇算法虽然年代久远（2015年，two-phase algorithm），但确实一篇比较经典的 fuzzy utility algorithm，需要好好研究一番

Fuzzy utility mining with upper-bound measure

样例

Fuzzy Method

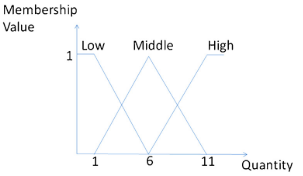
Transaction Dataset

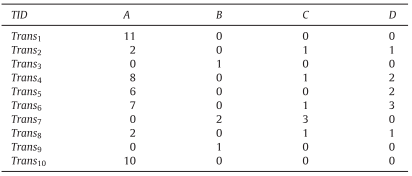
Utility of Each Item

定义

• 项集（itemset）：由 $I=\lbrace i_1, i_2, \ldots, i_n \rbrace$ 中的多个项组成的子集 $\lbrace i_1, \ldots, i_l \rbrace$，且 $1 < l \le n$，$i_j \not= i_k$($j \not= k$)； $l$ 表示的是该项集的长度，我们称为 $l$-$itemset$

• 量化交易项集（quantitative transaction database）：量化交易项集（QDB）由许多条交易项组成 $\lbrace Trans_1, Trans_2, \ldots, Trans_y, Trans_z \rbrace$，其中下标指代每条交易项的编号（TID），$z$ 表示该 QDB 中总共有多少条交易项

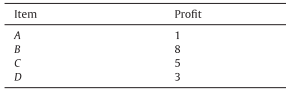
• 模糊集合（fuzzy set）：每条交易项都是由许多 itemset 组成，在交易项 $Trans_y$ 中项 $i_z$（下标代表第几个）的模糊量化值 $f_{yz}$ = $\big($ $\frac{f_{yz1}}{R_{z1}}$+$\frac{f_{yz2}}{R_{z2}}$+$\dots$+$\frac{f_{yzl}}{R_{zl}}$+$\dots$+$\frac{f_{yzh}}{R_{zh}}$ $\big)$，其中 $R_{zl}$ 指的是项 $i_z$ 属于哪些模糊区间（本文中是 $Low$，$Middle$ 和 $High$，$f_{yzl}$ 同理），$i_z$ 在 $Trans_y$ 中的数量用 $v_{yz}$ 表示。比如项 $D$ 在 $Trans_6$ 中模糊集合的量化值为 $f_{6,D}$=$(0.6/D.Low, 0.4/D.Middle, 0/D.High)$

  Ps. 0.6、0.4 和 0 这三个数字来源于第一个样例（Fuzzy Method），因为垂直于Quantity轴的直线会至多与两个模糊区间相交，所以在本文中一个项的模糊集量化值至多同时存在两个，计算方式可以看作是求解相似三角形

• 利润值（external utility）：每个项都有一个唯一的正效用值，为了方便理解通常称为利润值，使用 $s(i_z)$ 表示（若为负数又会如何处理呢？）

• 在某条交易项上项的模糊效用值（fuzzy utility of item in a transaction）：思路和一般项的效用值计算方式一致，在模糊效用挖掘中计算公式为 $fu_{yzl}$=$f_{yzl} \times v_{yz} \times s(i_z)$；同样以在 $Trans_6$ 中的项 $D$ 为例，$f_{6,D}$=$0.6 \times 3 \times 3$，而求解在整个数据集中项所有的模糊效用在之后介绍

• 在某条交易项上项集的模糊效用值（fuzzy utility of itemset in a transaction）：同样是在某条交易项中，$fu_{yX}$=$f_{yX}$ $\times$ $\sum_{R_{yzl} \subseteq X}$$(v_{yz} \times s(i_z))$，需要特别指出 $f_{yX}$ 是取在项集 $X$ 所有项元素 $i_z$ 中，其模糊量化值最小的作为该值进行计算；比如在 $Trans_6$ 中，模糊项 $C.Low$ 和 $D.Low$ 的模糊量化值分别是 $1$ 和 $0.6$，那么 $f_{6,\lbrace C.Low, D.Low \rbrace}$=$0.6$

• 项的模糊效用值（fuzzy utility of item）：在整个数据集中，项的模糊效用值计算公式为 $afu_z$=$\sum_{i_{zl} \in y}fu_{yzl}$

• 项集的模糊效用值（fuzzy utility of itemset）：在整个数据集中，项集的模糊效用值计算公式为 $afu_X$=$\sum_{y}fu_{yX}$；同样以项集 $X$=$\lbrace C.Low, D.Low \rbrace$ 为例，$afu_X$=$fu_{2,X}$+$fu_{4,X}$+$fu_{6,X}$+$fu_{8,X}$=$33.2$

• 高模糊效用项集（high fuzzy utility itemset）：当某个项集的模糊效用值不小于给定的阈值 $\lambda$，那么我们称该项集是高模糊效用项集（HFU）

• 在某条交易项上项的最大模糊效用值（maximal fuzzy utility of item in a transaction）：因为在一条交易项集上存在许多模糊区间，所以对某个项 $i_z$ 必然是有一个最大的模糊量化值和最小的模糊量化值，文中取最大的模糊效用值作为上边界预估值计算，达到 downward-closure property 的效果

• 交易项的最大模糊效用值（maximal fuzzy utility of a transaction）：因为有项的最大模糊效用值，自然由多个项组成的交易项自然也有最大模糊效用值，计算公式为 $mtfu_y$=$\sum_{i_z \subseteq Trans_y}mfu_{yz}$

• 模糊效用上边界（fuzzy utility upper-bound）：根据交易项的最大模糊效用值来求上边界（预估值，类似于 $TWU$）可以求得项集 $X$ 的预估值 $fubb_X$=$\sum_{X \subseteq Trans_y \subseteq QDB}mtfu_y$

• 候选高模糊效用项集（high fuzzy utility upper-bound itemset）：当一个项集的模糊效用上边界值不小于阈值 $\lambda$ 时，该项集有可能是 HFU，还需要进一步计算核实

算法

TPFU Algorithm

总结

TPFU算法没有使用到很厉害的剪枝策略或者其它计算方法，因为是属于经典的 two-phase 类算法，所以阅读伪代码并没有很大的难度。个人有以下几点疑问：1）在 Phase I 过程中，反复遍历 QDB，在实际代码中也是如此吗？2）只使用一个 upper-bound 是不是会让边界值显得不够紧凑？3）有没有更高效的方法计算各种最大值？4）在实际代码中是用数组还是hashmap存储这些数据？文中也提到，FUM 不同于之前研究的 HUEM 那般简单，更多的是为了得到有用的关联规则，用 ”很小、小、合适、大、很大“（Membership Function） 这样的形容词代替精准的数字，更符合我们日常生活中的描述习惯，但随之而来的就是求解步骤更加繁琐，具体细节还需要进一步研究代码