写在前面：该算法针对UP-Span算法做出了很多改进，把候选项集数量给大大减少，也是在UP-Span算法的基础上进一步优化的结果，整体的设计思路是一致的。亮点在于设计了有序prefix-tree这种存储结构，使得挖掘过程中的信息能够得到有效保存而且无需重复计算，更重要的是，该算法提出两个比EWU更为紧凑的上界，很大程度上缩小了检索空间

High Utility Episode Mining Made Practical and Fast

样例

Complex Event Sequence

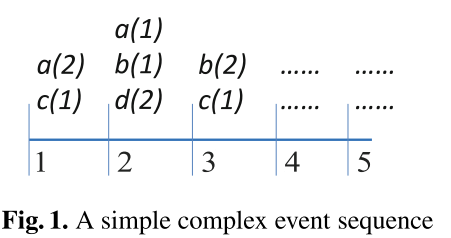
External Utility of Events

定义

大部分基础定义可以参考 UP-Span 这篇算法，这里仅给出一些补充：

• 一个情节的效用定义为 $u(\alpha) = \sum_{mo(\alpha) \in moSet(\alpha)}u(\alpha, \, mo(\alpha)) / u(CES)$，其中 $mo(\alpha)$ 指的是情节 $\alpha$ 在整个事件序列上出现的最小时间段/点（minimal occurrences，比如说一个人在一天三个不同时间点花同样长的时间吃饭）；$u(CES)$ 指的是整个复杂事件序列的总效用值，这里采用比率的形式来增加可信度

• MTD（maximum time duration）就是时间窗口，指特别规定只考虑在这个时间长度内发生的事件之间的关联规则，否则工作量会无穷大，而且得到结果的时效性也没那么强

• 情节权重效用（Episode Weighted Utility）类似于 TWU，单个情节 $\alpha$ 的 $EWU(\alpha)$ 计算公式为： \(EWU(\alpha, mo(\alpha)) = \sum_{\rm i = 1}^{\rm n}u(SE_{\rm i}, \, T_{\rm i}) + \sum_{\rm i = e}^{\rm s+MTD-1}u(CES_{\rm i}, \, T_{\rm i}) \\ EWU(\alpha) = \sum_{\rm i=1}^{\rm k}EWU(\alpha, \, mo(\alpha)_{\rm i}) / u(CES)\) Ps. 因为 $mo(\alpha) = [T_{\rm s}, \, T_{\rm e}]$，所以 $s$ 是起始时间点，$e$ 是终止时间点，需要明白 $EWU(\alpha, mo(\alpha))$ 的计算意义（可以类比 TWU/SWU 进行理解）

• 对情节的拓展采用方式是把事件逐个添加到尾部，当时间跨度没有发生变化时，称为 I-Concatenation，当时间跨度变长时，称为 S-Concatenation

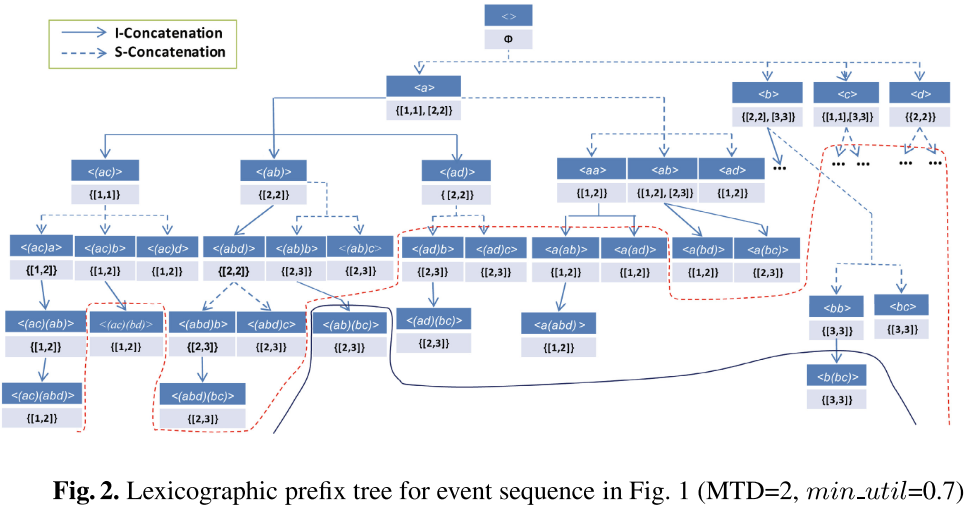
• 有序前缀树（lexicographic prefix tree）根据上一条定义的拓展方式，从根节点逐步构造出一棵含有完整信息的树，每个节点之间都是有序的，示意图如下：

  

  Ps. 可以明显看得出来这棵树在没有剪枝的情况下是非常大的，对此我们可以把构造过程进行拆分，把这棵大树拆成四棵局部小树（根节点为 a、b、c、d），然后对每棵小树依然可以采用同样的方式（相当于空间换时间）黑色实线是使用EWU进行的初步剪枝效果，红色虚线是该算法采用的新上边界剪枝策略产生的效果

策略

Improved EWU for I-Concatenation

简称“IEIC”，是在 I-Concatenation 方法之前得到的一个新的上边界，通过这个上边界，I-Concatenation就可以避免对情节 $\alpha$ 的效用值进行重复计算，计算公式如下： \(IEIC(\alpha, \, mo_{\rm i}(\alpha)) = \sum_{\rm j = 1}^{\rm k}u(SE_{\rm j}, \, T_{\rm j}) + u(IES_{\rm i}(\alpha)) + u(SES_{\rm i}(\alpha)) \\ IEIC(\alpha) = (u(\alpha) + u(IES(\alpha)) + u(SES(\alpha))) / u(CES)\) 其中，$IES(\alpha)$ 是计算在情节 $\alpha$ 内，排在当前事件之后的剩余事件的总效用值，$SES(\alpha)$ 是计算情节 $\alpha$ 后续事件序列的效用值（utility of events in subsequent，$CES_{\rm i}$）

Improved estimation of EWU for S-Concatenation

简称“IESC”，是在 S-Concatenation 方法之前得到的一个新的上边界，通过这个上边界，S-Concatenation可以得到相同的效果，因为它是串行连接，所以考虑因素更少，计算公式如下： \(IESC(\alpha) = (u(\alpha) + u(SES(\alpha))) / u(CES)\)

算法

I-Concatenation

可以看作是并行连接，这个过程简单一些，只要把新的事件 $\beta$ 直接挂在情节 $\alpha$ 尾部即可，需要注意的是他们的结束时间 $T_{\rm e}$ 必须保持一致

S-Concatenation

可以看作串行连接，但更复杂一些，需要筛去重叠的时间段，避免重复计算，其它过程的思路和并行连接一致

Prefix-Growth

论文中起了另外一个名字 $TSpan$，也是本算法的简称

总结

TSpan算法有些证明过程被省略了（我找到的可能是会议版）。从实验结果上来看比UP-Span要好很多，而且提出的这两个新的上边界确实能够起到很大的筛选作用（不过我看着怎么这么像HUI-Miner和EFIM中的剩余项效用边界，remaining utility upper bound）而且我注意到在测试数据集的平均长度偏大的时候，生成的候选节点数和运行时间都是陡直上升，这说明剪枝还是不够充分，最为困难的是事件组合不同于项集组合那般容易。我想可以考虑只对串行或并行进行剪枝优化，但这样会不会因为剪掉了一些节点而影响到另一个挖掘进程？