写在前面:序列挖掘比单纯地效用挖掘更具广泛性,因为加上时间维度才是我们日常生活经常碰到的问题,当然这也会使得问题更加复杂。通过学习USpan算法,可以初步了解序列挖掘是一个怎么样的过程,为后续研究做个基础。
An Efficient Algorithm for Mining High Utility Sequential Patterns
样例
quality of items

sequence database

定义
效用值定义与 HUI-Miner 中对项、项集、交易项和数据集的效用值计算方式是一致的,这里仅作一些补充:
项(item)定义为 $i_{\rm k} \in I$ ($1 \le k \le n$),单个项的效用值定义为 $p(i_{\rm k})$,其在某个序列中的数量是 $(i_{\rm k}, q)$
项集(itemset)定义为 $l = [(i_{\rm j_1}, q_1), \ldots, (i_{\rm j_{\rm n}}, q_{\rm n})]$,需要注意论文中对长度只有1的项集表现形式是不带方括号,而且项集中的每个项是按照字母顺序排列
序列(sequence)是由一系列项集构成,$s = \big< l_1, l_2, \ldots, l_{\rm m} \big>$
序列数据集(sequence database)是多个序列构成,为了区分序列,给每个序列赋予唯一的ID,如上面样例中的 Table 2
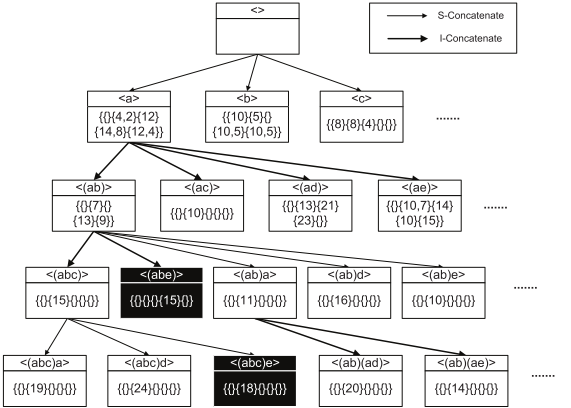
项、项集和序列之间的顺序通常按照字母顺序排列,其中 I-Concatenate(并行扩展,序列大小无变化)和 S-Concatenate(串行扩展,序列大小加一)
论文中的例子如下:
- 原序列-$\big<ea\big>$ 大小为2, $\big<e(ab)\big>$:I-Concatenate,扩展后序列大小依然为2;$\big<eab\big>$:S-Concatenate,扩展后序列大小为3
- 当序列 $t_{\rm a}$ 是序列 $t$ 基于 I-Concatenate 得到的,$t_{\rm b}$ 是基于 S-Concatenate 得到的,那么 $t_{\rm a} < t_{\rm b}$
- 当序列 $t_{\rm a}$ 和 $t_{\rm b}$ 是基于同一种扩展方式得到的,对两个序列内的项按照字母顺序依次比较,如 $\big<(ab)\big> < \big<(ab)b\big>, \, \big<(ab)c\big> < \big<(ab)d\big>$
序列排序树(lexicographic q-sequence tree,LQS-Tree)按照以下规则构造:
根节点为空,每个节点都是一个序列,而且需要记录其效用值
任何节点都是通过对父节点 I-Concatenate 或 S-Concatenate 得到的
任何节点的所有子节点都按字母递增顺序列出

高效用序列(high utility sequential pattern)与高效用项集(HUI)还是有区别,因为在一个序列中会有多个重复的q-subsequence,如在 $s_5$ 中子序列 $\big<ea\big>$ 有 $\big<(e, 3)(a, 6)\big>, \, \big<(e,3)(a,2)\big>$ 和 $\big<(e,3)(a,2)\big>$,本算法规定使用最大的效用项值作为该子序列的效用值,即 $u_{\rm max}(\big<ea\big>, \, s_5) = \lbrace 3 \times 1 + 6 \times 2 \rbrace = \lbrace 15 \rbrace$,通用公式为 $u_{\rm max}(t) = \sum max \lbrace u(s^\prime) \mid s^\prime \sim t \land s^\prime \subseteq s \land s \in S \rbrace$,即 $u_{\rm max}(\big< ea \big>) = u_{\rm max}(\big< ea \big>, s_2)+u_{\rm max}(\big< ea \big>, s_4)+u_{\rm max}(\big< ea \big>, s_5) = 41$。当 $u_{\rm max}(t) \ge minUtil$ 则说明该序列是高效用序列
Ps. 为什么不采用累加的方式呢?是因为这是一个有序序列,累加并没有任何实际意义?可以想一想
剩余项效用(remaining utility of items)指在当前序列中,那些排在当前项之后的所有项的效用值之和,也就是下面 utility matrix 中每个 entry 中括号内右边的那个值($u_{\rm rest}(k, s_{\rm i})$)
Ps. 原论文中在 Section 4.4 中有详细介绍
策略
utility matrix
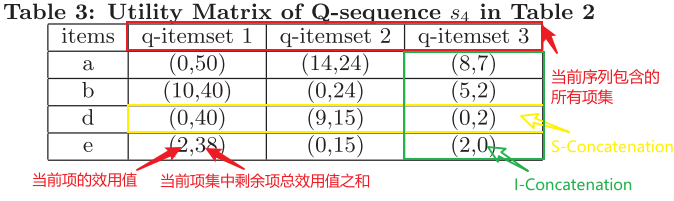
通过这张矩阵表,我们就可以得到组合信息(因为每次只扩展一位,所以一元项组成二元项集,二元项集组成三元项集…)举个例子:项 $b、e$ 进行I-Concatenation扩展得到 $\big< (be) \big>$,只需要将 q-itemset 1 和 q-itemset 3 这两列 $b$ 和 $e$ 的效用值加起来即可,即 $v(\big< (be) \big>, s_4) =\lbrace 10+2, \, 5+2 \rbrace$;若对 $\big< (be) \big>$ 进行S-Concatenation扩展得到 $\big<(be)a\big>$,可以从 Table 3 中找到 q-itemset 2: $\big<(b, 2)(e, 2)\big>$ 和 q-itemset 3: $\big<(b, 2)(e, 2)\big>$,即 $v(\big< (be)a \big>, s_4) = \lbrace 12+14, \, 12+8 \rbrace$(之所以没有 $\lbrace 7+14 \rbrace$ 是因为 q-itemset 之间有先后顺序,若计算 $\lbrace 7+8 \rbrace$ 那么得到的应该是 $\big<(abe)\big>$ 序列)
width pruning
主要作用在于筛选出尽可能少的候选项集以便作进一步过滤得到真正的高效用项集序列,基于 sequence-weighted downward closure property(SDCP),也就是 sequence-weighted utilization (SWU,计算方式和TWU一致,如 $SWU(\big< ea \big>) = u(s_2) + u(s_4) + u(s_5) = 41 + 50 + 37$)
定理:当序列 $t$ 有 $SWU(t) < minUtil$,那么以该序列为基础的所有扩展序列都是低效用序列,可以被剪枝(证明过程详见原论文 Section 4.3 部分)
depth pruning
在序列 $t$ 和 $S$ 中,有 $u_{\rm max}(t) < \sum {\rm i \in s^\prime \land s^\prime \sim t \land s^\prime \subseteq s \land s \in S}(u{\rm rest}(i, s) + u(s^\prime))$,所以当 $u_{\rm rest}(i, s) + u(s^\prime) < minUtil$,我们可以停止对当前节点进行深度挖掘,而是回溯到上一个节点。其中 $s^\prime$ 是该序列中第一个匹配子序列 $t$ 的序列,而对子序列 $t$ 的扩展也是从第一个匹配到的 $s^\prime$ 开始,把排在后面的项一个个使用 I-Concatenation 或 S-Concatenation 得到扩展后更长的子序列。如果从第二个匹配到的子序列开始扩展,它的效用值始终是低于第一个匹配到的子序列的扩展(因为可以扩展的项没有之前那么多)
算法

总结
USpan算法理解起来并不是很难,因为它没有采用过多的优化策略或复杂的存储结构,能够很清晰的让人理解什么是序列挖掘,基本的序列挖掘过程是怎么样的,原论文中对SWU这样的公式也有详细的证明和推理过程。但同时我也发现,该算法的测试数据集是基于transaction 形式,没有加上时间点这个参照物,不具备一般性,真正的扩展性并不强。