写在前面：该算法是基于 HUI-Miner 的 utility-list 结构设计的 top-k挖掘算法，其中采取的不少阈值自增策略是值得我们学习研究，写这篇笔记的目的也是为了介绍这些策略以及个人的想法

An efficient algorithm for mining the top-k high utility itemsets, using novel threshold raising and pruning strategies

样例

External utility of items

Example database

定义

大部分内容可以参考 HUI-Miner 这篇算法的笔记，这里仅做一些额外的补充

Estimated Utility Co-occurrence Structure (EUCS)

论文中把 EUCS 定义为一个元组（${(a;\ b;\ TWU(ab) )$，$a,b \in I^*$，$TWU(ab) \in R^+}$），其中 $a$ 和 $b$ 都是项（默认不重复）$R^+$ 说明该算法不考虑负效用想的情况。为方便理解，作者画了几个矩阵图来说明（Ps. 实际上是用hashmap存储这些信息，而不是真的用矩阵结构），具体构建过程如下图：

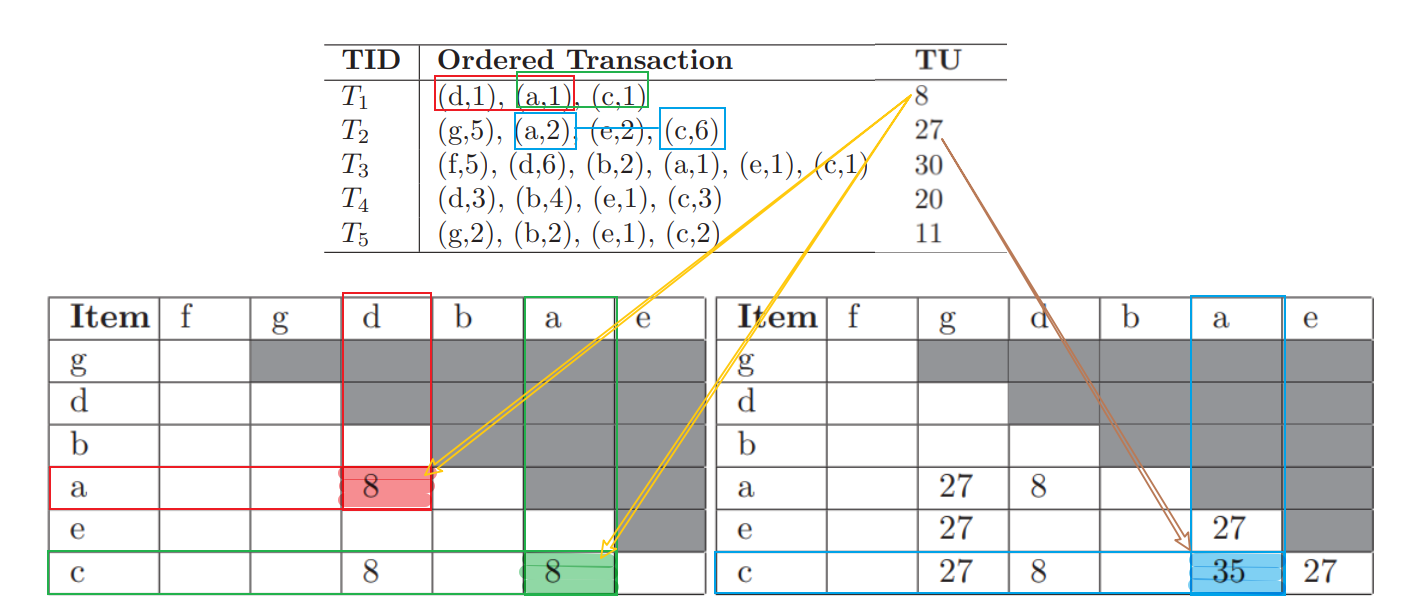
Utility list construction

• 项集效用值：在已经构建好的 utility list 中，求一个项集的效用值公式为 $\sum_{\rm ul \in UL(X)}ul.iutil$，其中 $UL(X)$ 指的是项集 X 的 utility list（如何构造可以参考 HUI-Miner）

Transitive extension upper-bound utility

给定任意一个项集 $X$ 和其可扩展项 $x$，新的边界值计算公式为 $teu(X, y)$ = $\sum_{\rm ul \in UL(X)}ul.iutil$ + $\sum_{\rm ul \in UL(y)}ul.iutil$ + $u(y)$

Coverage

当两个项 $i$ 和 $j$ 存在关系 $g(i) \subseteq g(j)$，我们称项 $j$ 包含（cover）项 $i$，则可以推导出有关项 $i$ 的覆盖 $C(i) = {g(i) \subseteq g(x) \land x \in I}$，其中 $g(x)$ 表示包含项 $x$ 的所有交易项的编号（TID），即 $g(x) = {tid \mid x \subseteq T_{\rm tid}}$

进一步拓展，项集之间也存在 coverage 关系，当项集 $X = x_1x_2 \ldots x_{\rm n}$，$x_{\rm i} \in C(x_1) (2 \le i \le n)$ 成立时，称 $X$ 是 coverage itemset

这其实是一个闭包概念？用少量的项代替后面与它有相同性质的扩展项集，接下来继续介绍根据 coverage 这个概念为基础得到的其它有用的性质，证明过程原文已有详细介绍，可以自己手动推导一下

• 性质1：令项 $i$ 和 $j$ 有 $j \in C(i)$ 关系，则有 $u(ij) \ge u(i) + \mid g(i) \mid \times p(j) > 0$，其中项集 $ij$ 是由两个项组合扩展得到
• 性质2：令项 $i$ 和 $j$ 有 $j \in C(i)$ 关系，则有 $TWU(i) = TWU(ij)$
• 性质3：令项集 $X = x_1x_2 \ldots x_{\rm n}$，则 $u(X) = \sum_{2 \le i \le n}u(x_1x_{\rm i}) - (n-1) \times u(x_1)$
• 性质4：根据 性质3，我们可以得到一个新的计算效用值的方式：设项 $x$，$x_i$ 和项集 $Y$ 有 $x_i \in C(x)$， $Y \subset C(x)$ 且 $x_i \not\in Y$，可得 $u(xYx_i)$=$u(xY) + u(xx_i)-u(x)$，同时我们可知 $u(xYx_i) > u(xY)$（参照 性质1 可推证）
• 性质5：根据 性质4，很容易就可以想到 $minUtil \le u(xY) < u(xYx_i)$ 是恒成立的（可以用闭包来解释？），论文中的规范表达为：设项 $j$，项集 $X$ 和 $Y$ 有 $Y \subseteq C(j)$，$X \cap Y = \varnothing$ 且 $j \not\in X$ 等关系恒成立，则 $minUtil \le u(jX) < u(jXY)$ 一定成立

策略

The estimated utility co-occurrence pruning strategy (EUCP)

在根据定义内容中的 EUCS 构造结束后，删除那些 $TWU(xy) < minUtil$ 的二元项，整理之后就可以得到一张 EUCST 结构图，如下图所示：

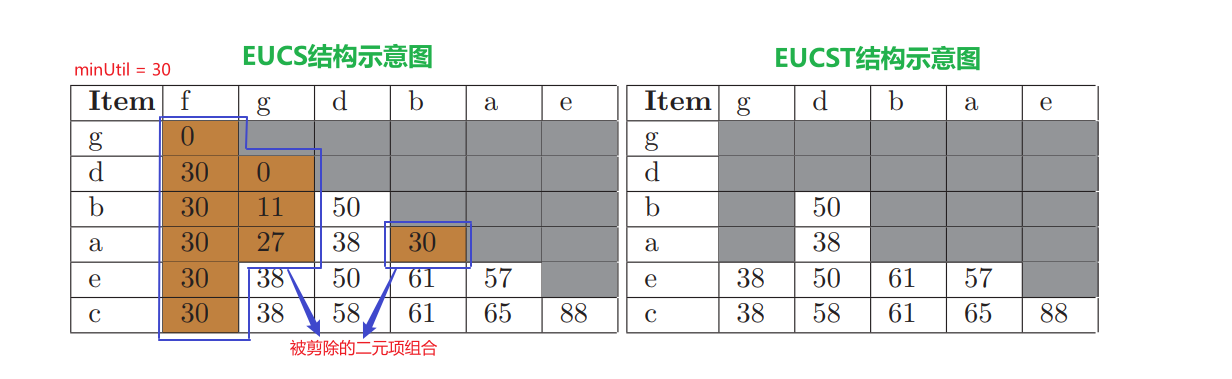
可以明显看出来，二元项集数量要比原来的要少很多，之后再在这个二元项集的基础上挖掘更高阶的高效用项集，这个剪枝策略核心还是使用传统的 $TWU$ 性质，但是以前的算法大多做到一阶项集剪枝，而该算法能成功在二阶项集上使用该性质，对其它算法而言具有很大的参考价值

The efficient utility-list pruning strategy

根据项集效用值计算和项集剩余效用值计算两个定义式，可以得到一个新的剪枝策略，即 $\sum_{\rm ul \in UL(X)}ul.iutil + \sum_{X \succ i}U(i) < minUtil$ 时，项集 $X$ 以及它的扩展集都不可能是高效用项集。原因在于在一条已经排序的交易项（transaction）中，排在项集 $X$ 之后的元素都将会成为 $X$ 的扩展项，若所有的扩展项效用值加起来都比阈值小，那自然单个组合的效用值也会小于阈值，所以可以直接剪除（证明过程在 HUI-Miner 中有详细论述）

The early abandoning additional strategy（EA）

• LA property：给定两个项集 $X$ 和 $Y$，当 $\sum_{\rm \forall T_i \in D}U(X, T_{\rm i}) + RU(X, T_{\rm i}) - \sum_{\rm \forall T_j \in D, X \subseteq T_{\rm j} \land Y \not\subseteq T_{\rm j}}U(X, T_{\rm j}) + RU(X, T_{\rm j}) < minUtil$ 时，则有 $\forall X \subseteq X^\prime \land Y \subseteq Y^\prime \Rightarrow X^\prime Y^\prime \not\in HUIs$

EA 策略的核心思想是遇到某个项集对 LA property 成立的话，就停止构造该项集的 utility list，以达到节省空间和时间的目的，证明推导过程在论文中有详细描述

Transitive extension pruning strategy (TEP)

根据 Transitive extension upper-bound utility 定义内容，存在以下两条性质：

• $teu(X, y) \ge u(Xy)$
• $teu(X, y) \ge \sum_{\rm ul \in UL(Xy)}(ul.iutil + ul.rutil)$

证明过程在论文中有详细推导，这里仅说结论。依据该性质，当 $teu(X, y) < minUtil$ 时，扩展项集 $Xy$ 和其后续扩展都是低效用项集，可以直接跳过对其构造 utility list （结合 The efficient utility-list pruning strategy）

Real item utilities threshold raising strategy (RIU)

这个策略在许多算法上都可以很轻松地实现，而且可以有不少变种。主要思想是扫描数据集的过程中，收集各个项的utility或者交易项集的utility，通常我们可以用 hashmap 存储这些值（因为之后的挖掘过程也可以使用）

The co-occurrence threshold raising strategy (CUD)

在EUCST的基础之上，利用 2-itemsets 的信息提高阈值，可以在其它算法上考虑一下是否也要构建一个CUDM来存储这些信息（有没有什么办法可以避免二次扫描数据集得出计算结果）

The coverage threshold raising strategy (COV)

主要是构造一个 COV List 来提升阈值，过程如下伪代码所示，个人认为该方法适用性会更强一些，因为涉及到的只有一元项

算法

construct utility list

在 HUI-Miner 里面有详细介绍，该方法的关键在于各个候选项有“共同前缀”才能进行拼接，但这种拼接方式其实效率很低，而且会产生很多无用候选项，所以在拼接操作之前要使得候选项尽可能地剪除那些低效用项

iConstruct algorithm

上面 utility list 构造算法其实效率很低，每次需要遍历(虽然是二分法)两个list，查找相同前缀的项集然后拼接起来，这个过程耗时而且占内存。kHMC 设计了一种新的构造方法，使用了EA策略避免构造那些低效用项集的情况

kHMC algorithm

整个算法的伪代码如下：

总结

kHMC 算法运用到了比较多的阈值提升策略，而且仅仅围绕 utility-list 结构展开，第一次接触到这篇论文只是粗略地扫过一遍，对运用到的方法和特性都没有仔细了解。作者也做了许多对比实验从各个方面测试了kHMC算法的优异性，同时也在结尾提到 coverage 这个概念其实可以在其它领域的效用挖掘同样使用。个人认为这篇算法还是有比较大的参考价值，值得研究。唯一不足的是没能在spmf上找到相关代码…