写在前面:Apriori算法与FP-Growth算法都是很经典的挖掘算法,自己也是断断续续地学习这两个算法。本文主要记录自己对这两个算法的理解和区别,有误的地方还请多多指教
辨析Apriori与FP-Growth
Apriori算法
Apriori 算法使用了逐层搜索的迭代方法,即用 k-项集探索 (k+1)-项集(后续的 HUI-Miner、FHN 和 UMEpi 等算法都是这个思路)。该算法使用了 向下封闭性(downward closure property),即一个频繁项集的所有非空子集也必须是频繁项集。假如项集 A 不满足最小支持度阈值,即 A 不是频繁的,则如果将项集 B 添加到项集 A 中,那么新项集(AUB)也不可能是频繁的
算法步骤
- 扫描数据集,确定每个一元项的支持度,通过计算得到的支持度,就可以得到所有频繁 1-项集的集合 F1;
- 使用上一次发现的 (k-1)-项集,两两组合产生新的候选 k-项集;
- 对得到的候选项集计算其支持度,再扫描一遍数据库,使用自己函数确定包含在每一个交易项t中的所有候 k-项集;
- 删除支持度小于阈值的所有候选项集;
- 重复 2~4 步骤,直到没有任何新的频繁项集产生时,算法终止

缺点
从上面的算法步骤可以看出,1)Apriori算法需要多次扫描数据集从候选项集中计算频繁项集的支持度,当数据集很大的时候,I/O开支就变得不可接受了;2)其次,在产生候选项集上是很庞大的,一般认为是 呈指数级增长,这对内存消耗和时间开支无疑是不可接受的
优点
毋庸置疑,Apriori算法作为最早也是最经典的频繁项集挖掘算法,使用先验性质,开创了一个新的挖掘思路;而且简单易理解,数据集要求低;最后,该算法在实际中得到广泛的运用,能够挖掘出很多有用的关联规则
FP-Growth算法
FP-Growth算法 针对 Apriori算法 的种种问题作出了许多改进,尤其是设计的 FP-Tree 结构来存储关键信息,借用 Tree 可以避免再去扫描数据集来确认结果(后续的 UP-Growth 、UP-GNV 和 RFM-Growth 等算法都用到了这个存储结构)。通过递归调用 FP-Growth 的方法可直接产生频繁模式,因此在整个发现过程中也不需产生候选模式
算法步骤
- 扫描数据集,以频繁一元项为基础构建有序项表头,并在第二次扫描数据集过程中对各个项元素进行排序;
- 根据项表头和排序调整后的数据集,构建 FP-Tree存储结构
- 按项表头内元素自底向上(同时也意味着FP-Tree自底向上)进行构建高阶项集,每一个高阶项集就是一条树枝路径
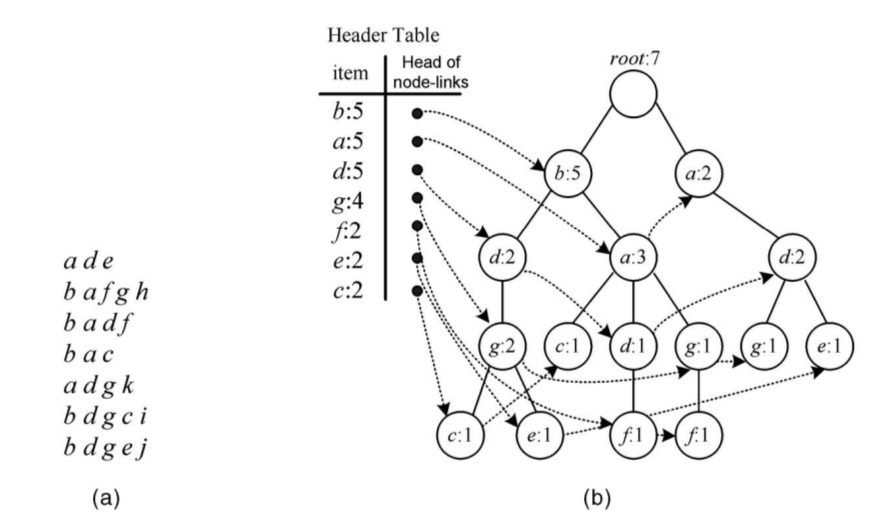
缺点
剪枝不够彻底,用到的边界值其实还不够贴近真正的支持度
优点
FP-Tree是数据集的浓缩,里面不包含非频繁一元项的数据;每次查找频繁项集也不需要重复扫描数据集,只需要固定一个元素,从下往上依次遍历各个节点直到root构造出一棵 sub FP-Tree(投影)
总结
- 在核心思路上,
- Apriori算法是 使用两个低阶的频繁项集构建高阶的频繁项集
- FP-Growth算法是 使用一个低阶频繁项集作为前提,筛选出包含这个频繁项集的所有高阶频繁项集
- 在实现过程中,
- Apriori算法需要多次扫描数据集来确认频繁项集的支持度
- FP-Growth算法通过固定一个节点构造更多的子FP-Tree来挖掘频繁项集
- 两个算法代表了不同的挖掘思路,根据这些思路可以结合不同的剪枝策略、存储结构等得到更高效的算法
Ps. 除了研究这些算法的性能差异性,更多的还是要理清来龙去脉,为什么这个算法能够得到大家的认可?为什么大家不使用其它看起来性能比它好得多的算法?